Модель Гаммерштейна

Входной сигнал u(t) известен.

1. Если известна функциональная зависимость f(u(t)) – вид нелинейности, то вводим Z=f(u(t)). Идентификация сводится к определению параметров линейной части:

.

2. Функциональная зависимость f(u(t)) не известна. Строится таблица этой нелинейной зависимости. По этой таблице любой интерпретируемой формулой получаем аппроксимирующий полином нелинейности f^*(u(t)). Зная параметры аппроксимирующего полинома, вводим Z(t) =f^*(u(t)) и, снимая соответствующие ему y(t), решаем задачу идентификации:

.

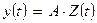Пример: Система приводится к следующему виду:

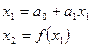- функция является нелинейной.

Используя метод интерполяции, аппроксимируем полином

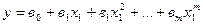
Составляем обобщенный вектор:

Тогда искомая матрица:

может быть получена по выражению:

,

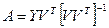где

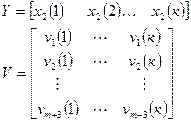
Метод Виннера

Является наиболее точным методом идентификации, на практике применяется крайне редко из-за сложности вычислений и отсутствия ясной физической интерпретации.