Двухэтапная процедура
1. Нелинейная характеристика разбивается на участки, в пределах которых нелинейная функция может быть с достаточной долей точности представлена линейной функцией. Данные участки называются участками линеаризации. Начало участков называется точкой линеаризации. В каждой точке линеаризации входной переменной придается незначительное приращение и фиксируется изменение выходной переменной. По данным входного и выходного переходного процесса с помощью линейных методов идентификации строятся линейные модели.
2. Аппроксимация линейных моделей в нелинейную функцию.
На основе зарегистрированного переходного процесса строится матрица коэффициентов линейным реверсионным методом. В результате получим столько матриц, сколько узловых точек. Каждый коэффициент матрицы аппроксимируется по той или иной интерполяционной формуле с помощью любого полинома.
Пример: Рассматривается отдельно нелинейное звено. На нелинейной характеристике выбирается отрезок, где система ведет себя как линейная функция.
 |
Рис. 23 График нелинейной функции
Отрезок, где функция линейна - 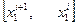 , где x1i – точки или узлы линеаризации.
, где x1i – точки или узлы линеаризации.
Для точек линеаризации подбираем соответствующие входные точки
 .
.
Каждой точке линеаризации подаем входную переменную, увеличивающуюся на величину 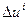
 .
.
Снимаем переходный процесс системы для каждой точки линеаризации.
Для каждой точки линеаризации получаем линейную модель Аi
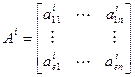
По каждому aij получаем функциональную зависимость aij = f(aij) методом аппроксимации тем же самым полиномом
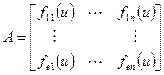 .
.
Планирование эксперимента
Пассивным экспериментом называют эксперимент, в котором регистрация входных и выходных данных осуществляется в рабочем режиме, не используя дополнительных вмешательств. Он применяется тогда, когда структура модели хорошо известна и ее адекватность не вызывает сомнений (когда решаются задачи параметрической идентификации).
Активный эксперимент предполагает особую программу проведения наблюдений таких, что позволяют по результатам исследований дополнительно оценить структуру модели.
Дата добавления: 2015-11-10; просмотров: 911;
