Разложение периодических функций в ряд Фурье

По определению периодической функцией называют функцию, отвечающую условию:

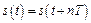, (8.1)

где T – период функции,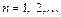

Для нахождения спектрального разложения функции s(t) введем в рассмотрение следующие наборы функций:

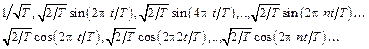(8.2)

Любая из функций (8.2), которую для краткости обозначим 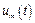, удовлетворяет условию периодичности (8.1).

Рассмотрим три следующие интеграла:

,

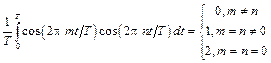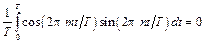, (8.3)

.

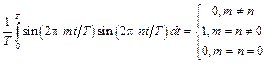Функции, удовлетворяющие условию (8.3), называются ортогональными, а систему функций (8.2) называют ортонормированным базисом, образованным гармоническими функциями с кратными частотами. Условие ортогональности можно записать в компактной форме, используя символ Кронекера:

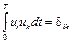, (8.4)

где

.

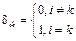Разложим произвольную периодическую функцию 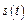в ряд

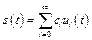. (8.5)

Представление (8.5) называется обобщенным рядом Фурье функции 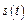в выбранном базисе.

Коэффициенты данного ряда находятся умножением (8.5) на базисную функцию 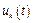и интегрированием по периоду функции :

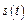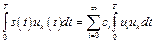. (8.6)

Откуда, используя свойство ортонормированности (8.4), найдем

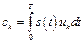. (8.7)

Подставляя в (8.7) набор функций (8.2), найдем значения коэффициентов ряда:

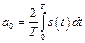, (8.8а)

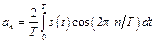, (8.8b)

. (8.8c)

Введя основную частоту 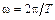последовательности, образующей периодическую функцию 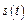, запишем ряд Фурье для периодического сигнала

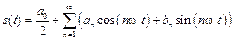. (8.9)

Анализ (8.9) показывает, что функция 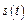содержит независящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых, гармоник с частотами 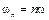( ), кратными основной частоте последовательности. Можно показать, что имеет место равенство

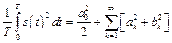(8.10)

Если записать коэффициенты ряда Фурье в виде

,

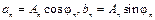где

,

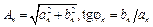то получим эквивалентную форму ряда Фурье:

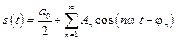. (8.11)

Спектральное разложение периодической функции 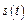можно выполнить используя систему базисных функций в виде экспонент с мнимыми показателями:

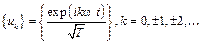, (8.12)

которые, как легко убедиться, вычислив интеграл

,

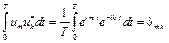являются ортогональными.

Ряд Фурье в данном случае принимает вид

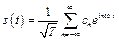(8.13)

с коэффициентами

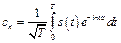. (8.14)

На практике принято использовать и другую форму записи ряда Фурье:

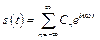, (8.15)

где

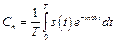. (8.16)

Выражения (8.13) – (8.16) представляют собой ряд Фурье в комплексной форме. Спектр функции 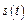в соответствие с формулами (8.15), (8.16) содержит компоненты на отрицательной полуоси частот, причем 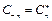, поэтому слагаемые с положительными и отрицательными частотами объединяются в пары, например:

.

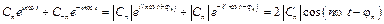Таким образом, отрицательная частота является не физическим, а математическим понятием, вытекающим из способа представления комплексных чисел.

Отметим, что в технической литературе, посвященной анализу сигналов, задачу вычисления коэффициентов разложения функции в ряд Фурье называют задачей анализа, а задачу восстановления функции по известным коэффициентам ряда Фурье - задачей синтеза.