Длительности

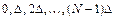Рассмотрим особенности спектрального представления дискретной функции, заданной на временном интервале конечной длительности [0,T] N отсчетами , взятыми соответственно в моменты времени . Полное число отсчетов .

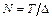Можно показать, что для дискретной последовательности коэффициенты ряда Фурье определяются формулой

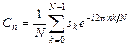. (8.21)

Формула (8.21) определяет последовательность коэффициентов, образующих дискретное преобразование Фурье (ДПФ), которое имеет следующие свойства:

1. ДПФ есть линейное преобразование.

2. Число коэффициентов 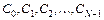, вычисляемых в соответствие с (8.21) равно числу отсчетов дискретной последовательности.

3. Коэффициент 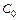(постоянная составляющая), есть среднее значение дискретной последовательности.

4. Если N – четное число, то

.

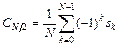5. Для вещественной дискретной последовательности, коэффициенты ДПФ, номера которых расположены симметрично относительно 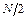, образуют сопряженные пары:

,

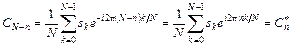поэтому можно считать, что коэффициенты 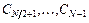отвечают отрицательным частотам.

Если для дискретной последовательности 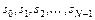найдены коэффициенты ДПФ 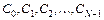, то восстановление исходной дискретной последовательности может быть осуществлено по формуле

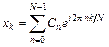. (8.22)