Основные сведения и определения

Определение 9.1. Дифференциальным уравнением 1-го порядка называют соотношение вида

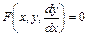. (9.1)

Определение 9.2. Дифференциальное уравнение вида

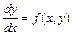, (9.2)

где 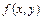- заданная функция двух переменных, называется дифференциальным уравнением первого порядка, разрешенным относительно производной.

Определение 9.3. Решением дифференциального уравнения на интервале I называется непрерывно дифференцируемая функция , превращающая уравнение в тождество на I.

Для дифференциального уравнения первого порядка (9.1), (9.2), по определению получаем

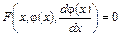, (9.3)

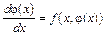. (9.4)

Определение 9.4. Соотношение (9.3) называется решением уравнения (9.4) в неявной форме (или интегралом уравнения (9.2)), если оно определяет y как функцию от x: , которая есть решение уравнения (9.2).

Определение 9.5. График решения уравнения (9.2) называется интегральной кривой данного уравнения.

Определение 9.6. Проекция графика решения на ось ординат называется фазовой кривой или траекторией дифференциального уравнения.

Определение 9.7. Задача о нахождении решения уравнения (9.2), удовлетворяющего начальному условию , называется задачей Коши.

Определение 9.8. Через каждую точку 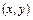из области определения уравнения (9.2) проведем прямую, тангенс угла которой к оси абсцисс равен 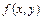. Данное семейство прямых называется полем направлений, соответствующим уравнению (9.2) (или полем направлений функции ).

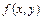Интегральная кривая в каждой своей точке касается поля направлений функции .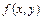

Существование и единственности задачи Коши дифференциального уравнения (9.1), (9.2) обеспечивается теоремой Пикара.

Теорема Пикара. Если функция f определена и непрерывна в некоторой области G, определяемой неравенствами

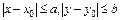(9.5)

и удовлетворяет в этой области условию Липшица по y:

, (9.6)

то на некотором отрезке 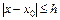, где h - положительное число, существует, и притом только одно решение уравнения (9.2), удовлетворяющее начальному условию .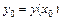

Здесь M - константа Липшица, зависящая в общем случае от а и b. Если 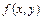имеет в G, ограниченную производную , то при 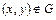можно принять

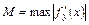. (9.7)

Определение 9.9. Дифференциальным уравнением n-го порядка называют соотношение вида

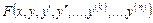=0, (9.8)

x - независимая переменная, неизвестная функция аргумента x, 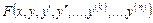- заданная функция переменных .

Определение 9.10. Задача о нахождении решения уравнения (9.8), удовлетворяющего начальным условиям

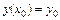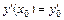, , …, , (9.9)

где 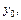, …, - заданные числа, называется задачей Коши для системы дифференциальных уравнений.

Дифференциальное уравнение n-го порядка заменой

,

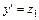, (9.10)

…

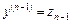
сводится к системе дифференциальных уравнений первого порядка:

,

,

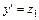… (9.11)

.

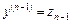
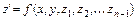Например, уравнение второго порядка

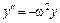(9.12)

можно записать в виде двух уравнений

,

. (9.13)

Методы решений дифференциальных уравнений подразделяются на три основные группы:

1. Аналитические методы решения.

2. Графические методы.

3. Численные методы.