Метод Пикара

Метод Пикара позволяет получить приближенное решение дифференциального уравнения (9.2) в виде функции, заданной аналитически.

Пусть в условиях теоремы существования требуется найти решения (9.2) с начальным условием 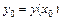. Запишем уравнение (9.1) в следующем эквивалентном виде

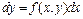. (9.14)

Проинтегрируем обе части (9.14) от 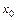до x:

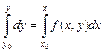. (9.15)

Вычислив интеграл в правой части, получим

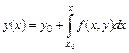. (9.16)

Очевидно, что решение интегрального уравнения (9.16) будет удовлетворять ДУ (9.2) и начальному условию 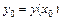. Действительно, при 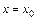получим:

.

Интегральное уравнение (9.16) позволяет использовать метод последовательных приближений. Положим 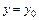и получим из (9.16) первое приближение:

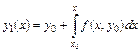. (9.17)

Интеграл, стоящий в правой части (9.17) содержит только переменную x, после нахождения этого интеграла будет получено аналитическое выражение приближения 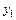как функции переменной x. Заменим теперь в уравнении (9.16) y найденным значением 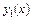и получим второе приближение:

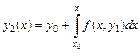(9.18)

и т.д.

В общем случае итерационная формула имеет вид:

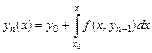
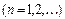(9.19)

Последовательное применение формулы (9.19) дает последовательность функций

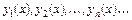(9.20)

Так как функция f непрерывна в области G, то она ограничена в некоторой области 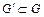, содержащей точку 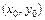, т.е.

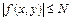. (9.21)

Применяя к уравнению (9.19) принцип сжимающих отображений можно показать, что последовательность (9.20) сходится по метрике 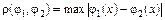в пространстве непрерывных функций j, определенных на сегменте 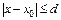, таких, что 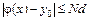. Предел последовательности является решением интегрального уравнения (9.16), а, следовательно, и дифференциального уравнения (9.2) с начальными условиями 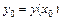. Это означает, что k-й член последовательности (9.20) является приближением к точному решению уравнения (9.2) с определенной степенью точности.

Оценка погрешности k-го приближения дается формулой:

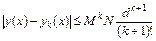, (9.22)

где M - константа Липшица (9.7), N - верхняя грань модуля функции f из неравенства (9.21), а величина d для определения окрестности 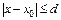вычисляется по формуле

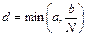. (9.23)