Определение 7. Дифференциал вектор-функции , вычисленный в точке , называется линейным перемещением точки из положения .

Дифференциал 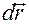вектор-функции 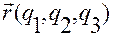, вычисленный в точке 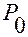, называется линейным перемещением точки из положения .

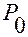Дифференциал 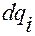криволинейной координаты называется линейным перемещением точки по обобщенной координате .

Дифференциал 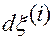контравариантной координаты 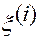называется линейным перемещением точки по контравариантной координате .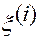

Линейное перемещение 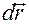, линейные перемещения 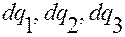, и линейными перемещения 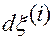по контравариантным координатам 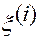связаны между собой следующими соотношениями

,

,

, .

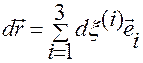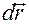
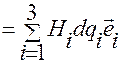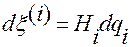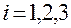Здесь коэффициенты Ламе 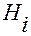и базисные векторы 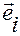, , 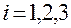вычисляются в точке .

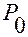Вывод этих соотношений описывается в дополнении к пункту 6, §5 этой главы в конце данной лекции.

7º. Союзная система координат и ее связь с основной. Ковариантные координаты вектора

Понятие ковариантных координат вектора

Пусть:

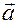— произвольный вектор;

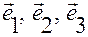— базис основной системы координат;

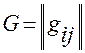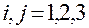, — матрица метрических
коэффициентов этой системы,

;

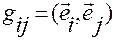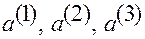— координаты вектора 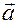в основной
системе как отмечено выше, они
называются контравариантными
координатами вектора .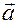

Введем следующее понятие.