Свойство 2

Векторы 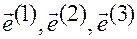линейно независимы, и для смешанного произведения этих векторов справедлива формула

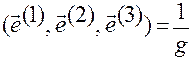. (1.5.18)

Для доказательства утверждения вычислим сначала векторное произведение векторов 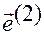и :

.

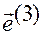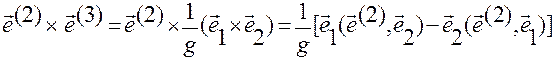В данной записи воспользовались третьей формулой в соотношениях (1.5.15)

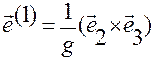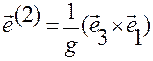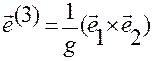, , (1.5.15)

и формулой двойного векторного произведения.

Согласно (1.5.17)

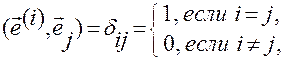(1.5.17)

справедливого для всех 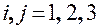, будем иметь

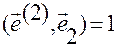и .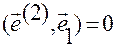

Поэтому окончательно находим

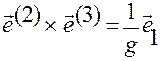. (1.5.19)

Подставляя (1.5.19) в смешанное произведение векторов 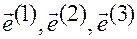и учитывая (1.5.17):

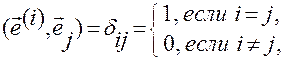(1.5.17)

для , получим

.

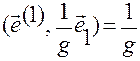Что и требовалось доказать.

Дополнение к §5 лекции 3 по главе 1.

В этом дополнении к §5 в пункте 6 дается понятие линейных перемещений точки, а также линейных перемещений в различных координатах (декартовых, контравариантных и криволинейных). Описывается их связь между собой.

§5. Задание движения материальной точки
в криволинейных координатах