Раскрытие неопределенностей. Правило Лопиталя
Будем говорить, что отношение двух функций 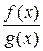 при
при 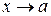 есть неопределенность вида
есть неопределенность вида 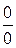 , если
, если 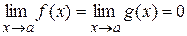 . Раскрыть эту неопределенность – значит вычислить предел
. Раскрыть эту неопределенность – значит вычислить предел 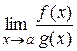 , если он существует, или установить, что он не существует.
, если он существует, или установить, что он не существует.
Теорема Лопиталя (Франсуа Лопиталь (1661-1704) – французский математик).
Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки 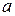 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки 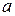 . Пусть, кроме того,
. Пусть, кроме того, 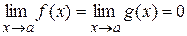 и
и 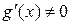 в указанной окрестности точки
в указанной окрестности точки 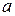 . Тогда, существует предел отношения производных
. Тогда, существует предел отношения производных 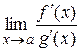 (конечный или бесконечный), то существует и предел
(конечный или бесконечный), то существует и предел 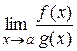 , причем справедлива формула
, причем справедлива формула
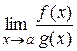 =
= 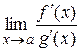 .
.
Замечание 1. Если производные 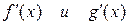 удовлетворяют тем же требованиям, что и сами функции, то правило Лопиталя можно применять повторно. При этом получается
удовлетворяют тем же требованиям, что и сами функции, то правило Лопиталя можно применять повторно. При этом получается 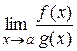 =
= 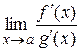 =
=  .
.
Замечание 2.Теорема остается верной и в случае, когда
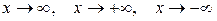 .
.
Примеры.
1) 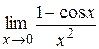 =
= 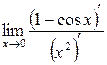 =
= 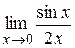 =
= 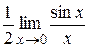 =
= 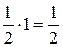 ;
;
2) 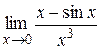 =
= 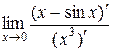 =
= 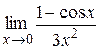 =
= 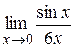 =
= 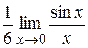 =
= 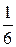 ;
;
3) 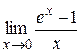 =
= 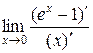 =
= 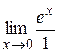 =
= 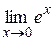 =1.
=1.
Будем говорить, что отношение двух функций 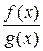 при
при 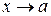 есть неопределенность вида
есть неопределенность вида 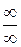 , если
, если 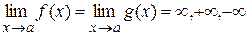 . Для этой неопределенности справедливо утверждение аналогичное теореме Лопиталя, если заменить условие
. Для этой неопределенности справедливо утверждение аналогичное теореме Лопиталя, если заменить условие 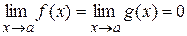 на условие,
на условие,
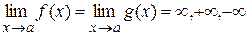 то теорема остается справедливой.
то теорема остается справедливой.
Примеры. 1) 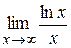 =
= 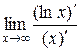 =
= 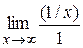 =
= 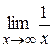 = 0.
= 0.
2)  =
= 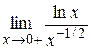 =
= 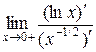 =
= 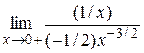 =
=
= 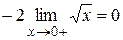 .
.
Неопределенности вида  и
и 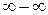 можно свести к неопределенностям
можно свести к неопределенностям 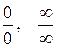 .
.
Дата добавления: 2015-08-21; просмотров: 895;
