Теорема Кантора. Следствие из теоремы Кантора
Теорема (Кантора). Пусть функция  определена и непрерывна на
определена и непрерывна на 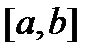 , тогда она равномерно непрерывна на
, тогда она равномерно непрерывна на 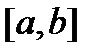 . (без доказательства).
. (без доказательства).
Определение 3. Пусть функция  определена и ограничена на
определена и ограничена на 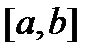 ,
, 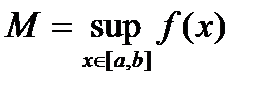 ,
, 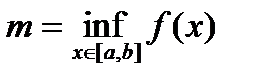 . Разность
. Разность 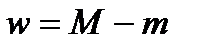 называется колебанием функции
называется колебанием функции  на
на 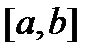 .
.
Следствие из теоремы Кантора. Пусть функция  определена и непрерывна на
определена и непрерывна на 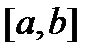 . Тогда для
. Тогда для 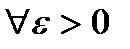 сегмент
сегмент 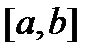 можно разбить на части таким образом, чтобы колебание функции
можно разбить на части таким образом, чтобы колебание функции  на каждой части было меньшим
на каждой части было меньшим 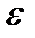 .
.
Доказательство. Поскольку  непрерывна на
непрерывна на 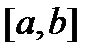 , то по теореме Кантора
, то по теореме Кантора  равномерно непрерывна на
равномерно непрерывна на 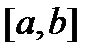 , т.е. для
, т.е. для 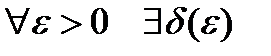 , что для
, что для 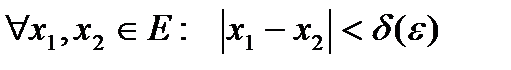 будет выполняться неравенство:
будет выполняться неравенство: 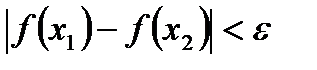 . Разобьем
. Разобьем 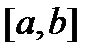 на части точками
на части точками 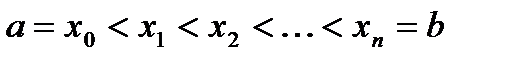 так, чтобы длины всех полученных частичных сегментов
так, чтобы длины всех полученных частичных сегментов 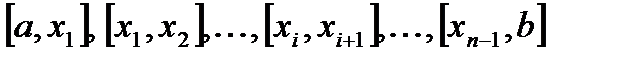 были меньшими
были меньшими 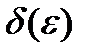 , т.е.
, т.е. 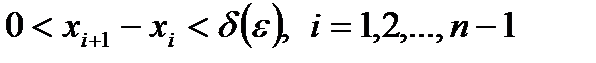 . Возьмем произвольный частичный сегмент из множества
. Возьмем произвольный частичный сегмент из множества 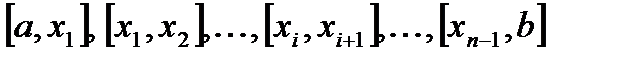 . Пусть этот сегмент -
. Пусть этот сегмент - 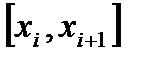 . На этом сегменте возьмем произвольно две точки:
. На этом сегменте возьмем произвольно две точки: 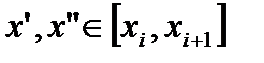 . Поскольку
. Поскольку 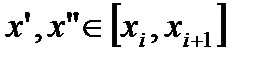 , то
, то 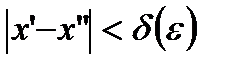 , а потому из условия равномерной непрерывности
, а потому из условия равномерной непрерывности  имеем, что
имеем, что 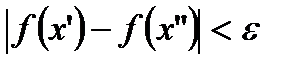 . Поскольку
. Поскольку  непрерывна на
непрерывна на 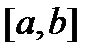 , то
, то  непрерывна на любом частичном сегменте
непрерывна на любом частичном сегменте 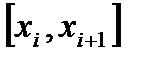 . По второй теореме Вейерштрасса
. По второй теореме Вейерштрасса  достигает на
достигает на 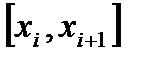 инфимума и супремума, т.е.
инфимума и супремума, т.е. 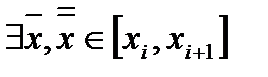 , что
, что
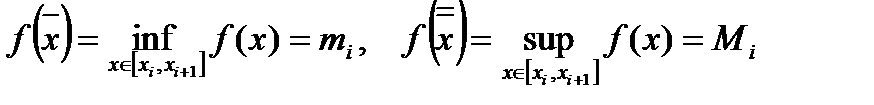 .
.
Колебание функции  на частичном сегменте
на частичном сегменте 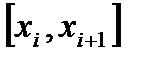 равняется:
равняется:
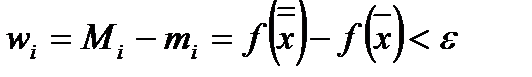 ,
,
что и нужно было доказать.
Вопросы
1. Понятие равномерной непрерывности функции. Чем равномерная непрерывность отличается от непрерывности функции?
2. Определение равномерно непрерывной на множестве функции.
3. Как связаны между собой непрерывность и равномерная непрерывность функции? Какое условие является более сильным? Объяснить.
4. Всегда ли из непрерывности функции на множестве вытекает ее равномерная непрерывность? В каком случае это происходит?
5. Теорема Кантора.
6. Определение колебания функции.
7. Чему равняется колебание функции 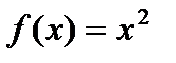 на сегменте
на сегменте 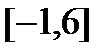 ?
?
8. Доказать следствие из теоремы Кантора.
Дата добавления: 2015-08-21; просмотров: 3229;
