Связь между непрерывностью и равномерной непрерывностью функции
Замечание 1. Если функция  равномерно непрерывна на
равномерно непрерывна на 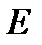 , то она непрерывна в каждой точке этого множества. Обратное, вообще говоря, не верно.
, то она непрерывна в каждой точке этого множества. Обратное, вообще говоря, не верно.
Действительно, пусть функция  равномерно непрерывна на
равномерно непрерывна на 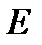 , тогда для нее имеет место определение 1. Переобозначим:
, тогда для нее имеет место определение 1. Переобозначим: 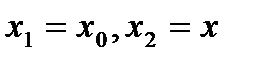 , тогда из определения 1 получим определение непрерывности функции
, тогда из определения 1 получим определение непрерывности функции  в точке
в точке 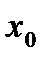 , которое базируется на определении предела функции по Коши.
, которое базируется на определении предела функции по Коши.
Замечание 2. Не любая функция  , непрерывная на множестве
, непрерывная на множестве 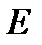 , будет равномерно непрерывной на этом множестве.
, будет равномерно непрерывной на этом множестве.
Определение 2. Функция  не будет равномерно непрерывной на
не будет равномерно непрерывной на 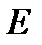 , если
, если 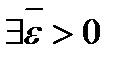 , что для
, что для 
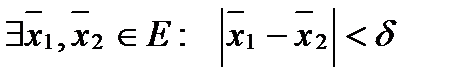 , а
, а 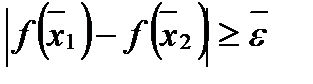 .
.
Пример. Доказать, что функция 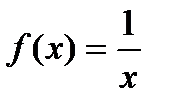 не будет равномерно непрерывной на множестве
не будет равномерно непрерывной на множестве 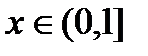 .
.
Заметим, что функция 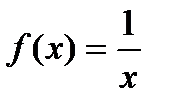 является непрерывной на
является непрерывной на 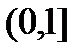 .
.
Возьмем 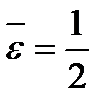 . Понятно, что для
. Понятно, что для  обязательно найдется
обязательно найдется 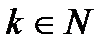 , что
, что 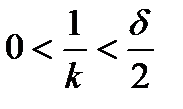 (действительно, для этого
(действительно, для этого 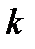 должно быть бóльшим
должно быть бóльшим 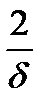 ). Тогда, если
). Тогда, если 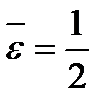 , то для
, то для 
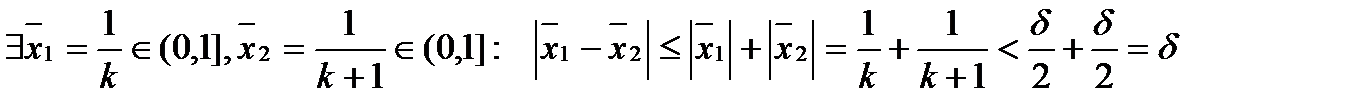 , а
, а 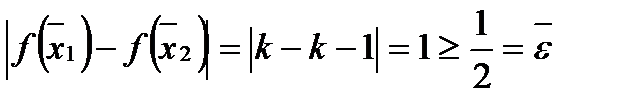 .
.
Таким образом, 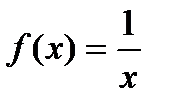 действительно не будет равномерно непрерывной на множестве
действительно не будет равномерно непрерывной на множестве 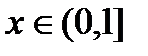 .
.
Дата добавления: 2015-08-21; просмотров: 1678;
