Понятие равномерной непрерывности функции

Лекция 8. Равномерная непрерывность функции

План

Понятие равномерной непрерывности функции

Связь между непрерывностью и равномерной непрерывностью функции

Теорема Кантора. Следствие из теоремы Кантора

Понятие равномерной непрерывности функции

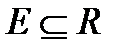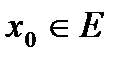Пусть функция определена и непрерывна на множестве , (рис.1). Поскольку 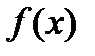непрерывна в точке 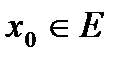, то по определению непрерывности функции на основе определения предела функции по Коши, это будет означать, что 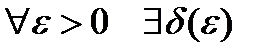, что для 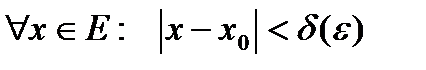будет выполняться неравенство: 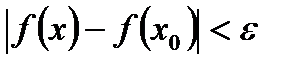. В точке 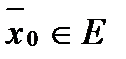функция также непрерывна, поэтому 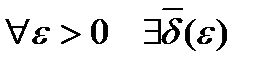, что для 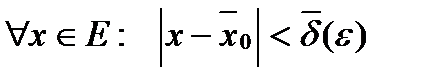будет выполняться неравенство: 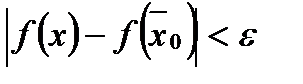. Заметим, что для одинакового 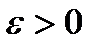для разных точек 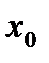и 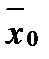, в которых является непрерывной, окрестности этих точек в общем случае разные: 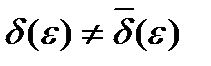, т.е. 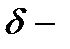окрестность зависит не только от 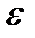, а и от точки 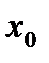, в которой рассматривается непрерывность. Таким образом, строгое определение непрерывности функции 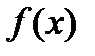в точке 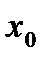будет выглядеть следующим образом: функция 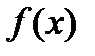непрерывна в точке 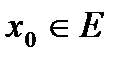, если для 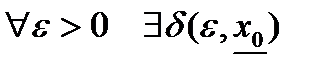, что для 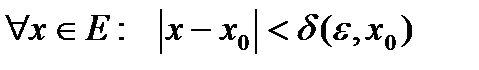будет выполняться неравенство: .

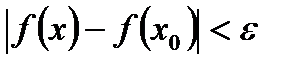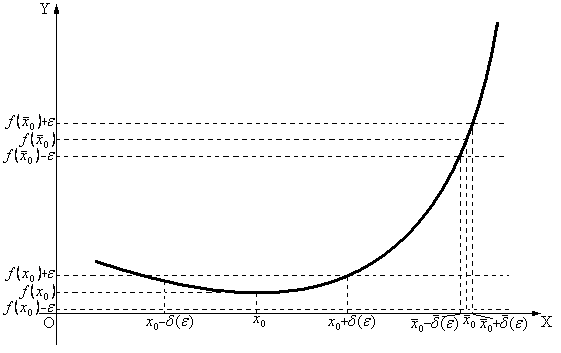
Рис.1.

Возникает вопрос: можно ли для 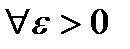найти 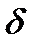так, чтоб оно подходило для 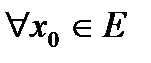одновременно? В этом случае такое 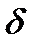будет зависеть лишь от 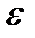и не будет зависеть от 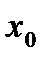, а потому может быть выбрано еще до выбора точки .

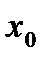Определение 1. Говорят, что функция равномерно непрерывна на 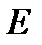, если для 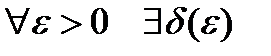(это 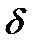зависит лишь от 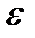и не зависит от 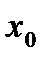), что для 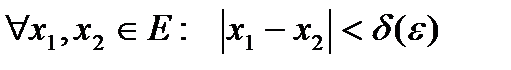будет выполняться неравенство: .

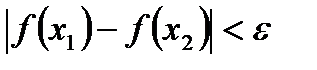Равномерная непрерывность означает, что во всех частях множества 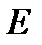достаточна одна и та же близость двух значений аргумента, чтобы достичь заданной близости соответствующих значений функции.