Обчислення потрійних інтегралів
Нехай 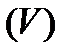 - прямокутний паралелепіпед
- прямокутний паралелепіпед 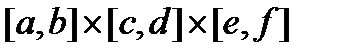 (рис.2), який проектується на YOZв прямокутник
(рис.2), який проектується на YOZв прямокутник 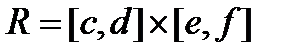 . Для такого
. Для такого 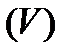 має місце наступна теорема.
має місце наступна теорема.
Теорема 2. Якщо для функції 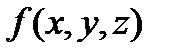 існує потрійний інтеграл
існує потрійний інтеграл 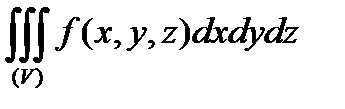 і для будь-якого фіксованого
і для будь-якого фіксованого 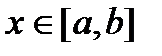 існує подвійний інтеграл
існує подвійний інтеграл
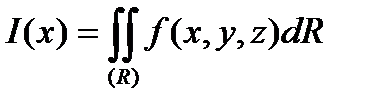 ,
,
то існує і повторний інтеграл:
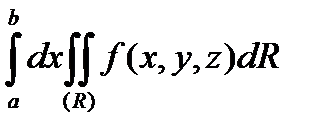
і

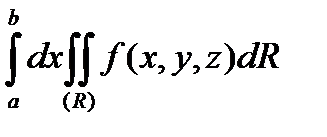 .
.
Якщо далі припустити, що для будь-яких 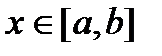 і
і 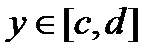 існує інтеграл
існує інтеграл 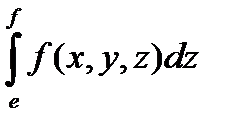 , то
, то

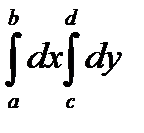
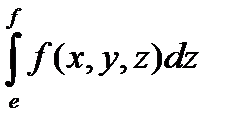 . (1)
. (1)
При потрібному існуванні інтегралів змінні в інтегруванні в формулі (1) можливо міняти місцями.
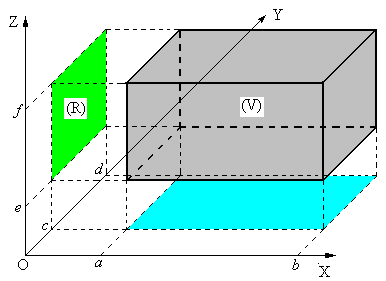
Рис.2.
Зауваження. Можна показати, що якщо існує потрійний інтеграл і інтеграл 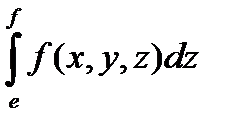 для будь-яких
для будь-яких 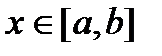 і
і 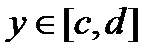 , то
, то
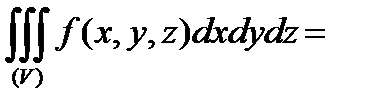
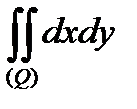
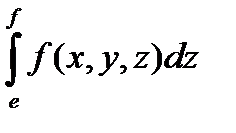 ,
,
где 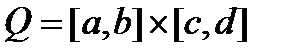 .
.
Нехай 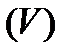 має довільну форму, функція
має довільну форму, функція 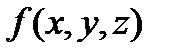 визначена на
визначена на 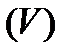 . Побудуємо
. Побудуємо 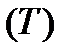 - прямокутний паралелепіпед, який містить у собі
- прямокутний паралелепіпед, який містить у собі 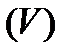 , і визначимо на ньому функцію
, і визначимо на ньому функцію 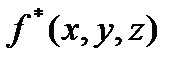 :
:
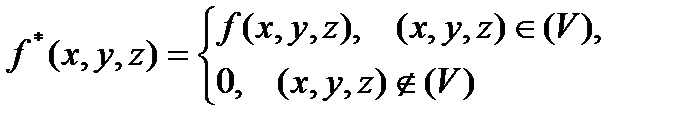
Цим шляхом отримаються всі нижчі формули.
Нехай тіло 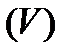 знаходиться між площинами
знаходиться між площинами 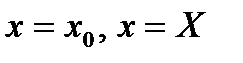 (рис.3), і кожною площиною
(рис.3), і кожною площиною 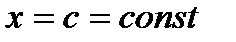 , перпендикулярною осі ОХ, де
, перпендикулярною осі ОХ, де 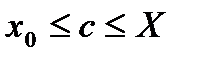 , перетинається по деякій фігурі з площею
, перетинається по деякій фігурі з площею 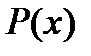 , проекцію якої на площину YOZпозначимо
, проекцію якої на площину YOZпозначимо  (рис.3).
(рис.3).
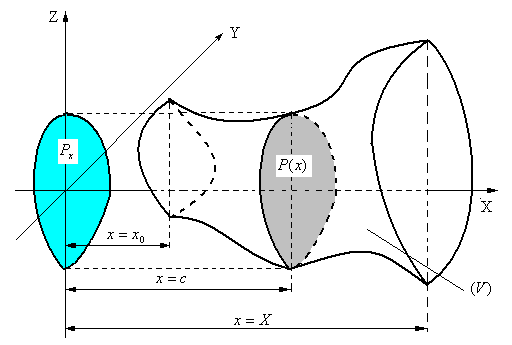
Рис.3
Тоді

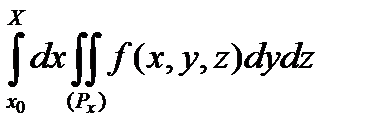 (2)
(2)
в припущенні існування подвійного і потрійного інтегралів.
Нехай 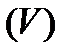 - циліндричний брус з твірною, паралельною осі OZ, обмежений знизу і зверху відповідно поверхнями (рис.4):
- циліндричний брус з твірною, паралельною осі OZ, обмежений знизу і зверху відповідно поверхнями (рис.4):
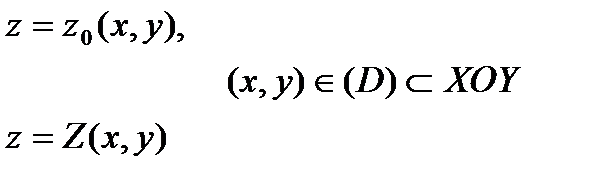
Тоді аналогічно (2) маємо:


 , (3)
, (3)
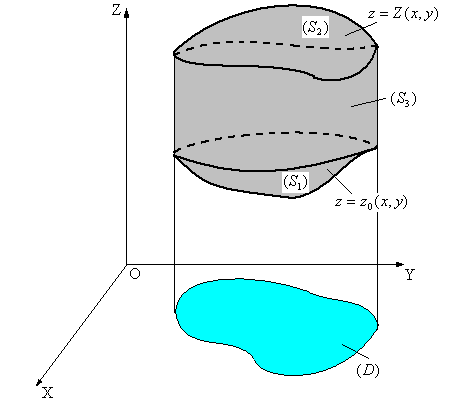
Рис.4.
якщо припустити існування потрійного і простого інтегралів.
 Приклад. Обчислити
Приклад. Обчислити 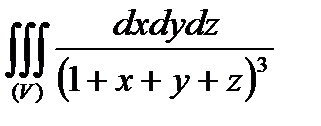 , де область
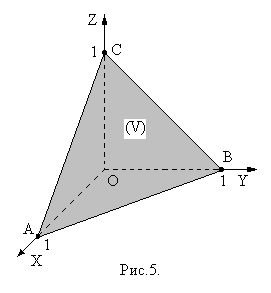
, де область 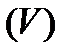 визначається наступним чином (рис.5):
визначається наступним чином (рис.5):
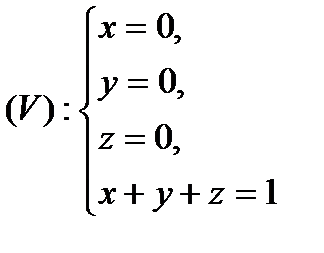
Тоді
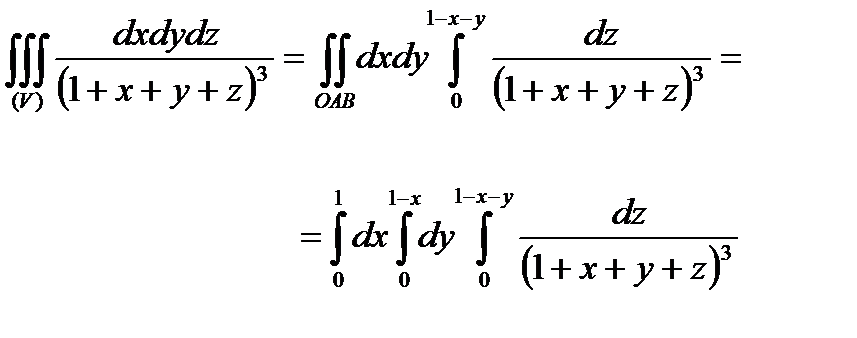 .
.
Дата добавления: 2015-08-21; просмотров: 2429;
