Критерий Коши сходимости несобственного интеграла І рода

При изучении свойств функции одной переменной было установлено, что для того, чтобы 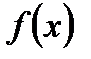имела предел в точке 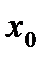необходимо и достаточно, чтобы она удовлетворяла условию Коши в этой точке, т.е. чтобы

для 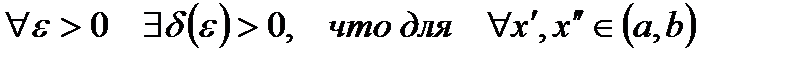таких, что 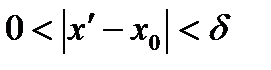, , 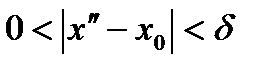выполняется неравенство:

.

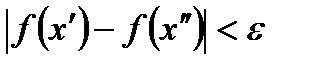Сходимость НИ І рода эквивалентна существованию предела (1) функции одной переменной 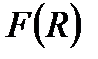. Таким образом:

если для выполняется неравенство

,

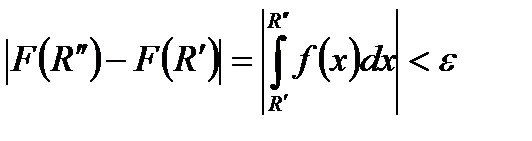то предел (1) суествует. Таким образом, мы доказали следующую теорему.

Теорема 1 (Критерий Коши сходимости несобственного интеграла І рода). Для того, чтобы сходился несвойственный интеграл I рода необходимо и достаточно, чтобы

: .

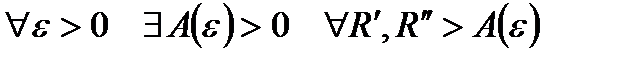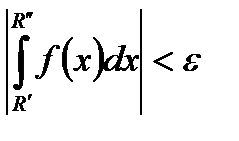3. Общее достаточное условие сходимости несобственного интеграла І рода

Теорема 2. Пусть функции 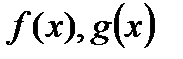определены на 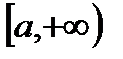и выполняются следующие условия:

1) , ;

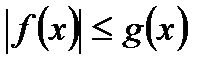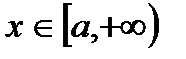2) 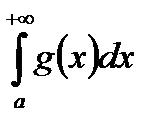- сходится,

то сходится и .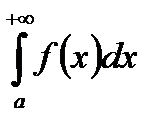

Доказательство. Из сходимости интеграла 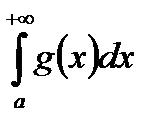по критерию Коши (теорема 1) вытекает, что

.

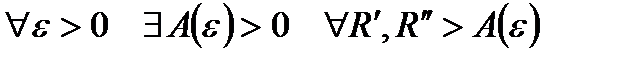
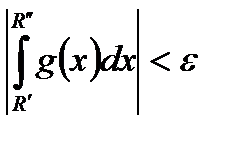Учитывая условие 1) теоремы, имеем, что функци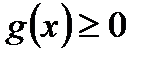я для 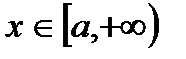, а это означает, что и 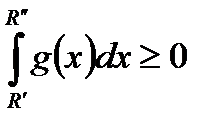, т.е. модуль в последнем неравенстве можно снять.

По свойствам интеграла Римана имеем:

.

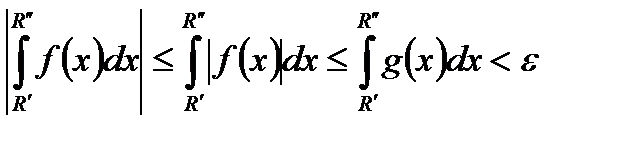Таким образом, для 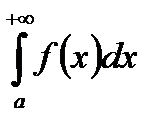имеем выполнение критерия Коши сходимости.

Пример. Рассмотрим несобственный интеграл 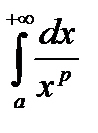, где 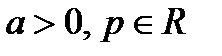. Выясним, при каких значениях параметра 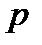этот интеграл является сходящимся. Пусть сначала 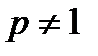. В этом случае:

.

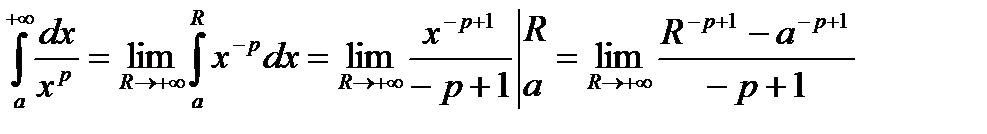Полученный предел существует, а интеграл сходится, если 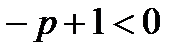, т.е. 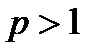. Если 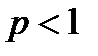, то интеграл расходится.

Осталось рассмотреть случай, когда :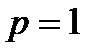

.

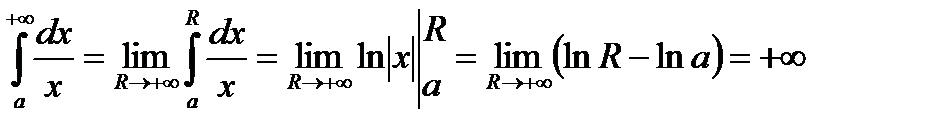Таким образом,

Вопросы

1. Определение несобственного интеграла І рода.

2. Условие Коши в точке для функции одной переменной.

3. Критерий существования предела функции одной переменной.

4. Когда несобственный интеграл І рода называется сходящимся (расходящимся)? Привести примеры сходящихся (расходящихся) несобственных интегралов.

5. Критерий Коши сходимости НИ І рода.

6. Как связаны сходимость (расходимость) интегралов ?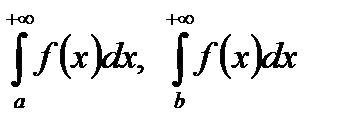

7. Общее достаточное условие сходимости несобственного интеграла І рода.