Предел функции нескольких переменных

Приведем определение предела функции двух переменных по Коши.

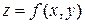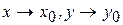Определение. Число А называется пределом функции при , т.е. в точке 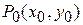, если для любого 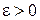существует 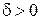, такое, что при всех , удовлетворяющих условиям | 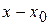| 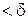и | 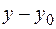| 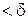, выполняется неравенство | 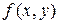— А| .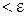

Данное определение в символьном виде можно записать так:

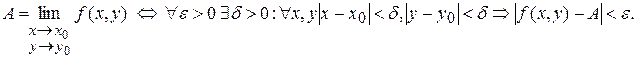
Для обозначения предела функции 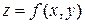в точке 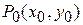используют и другую форму записи:

.

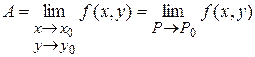Замечание.При определении предела функции 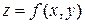в точке 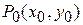полагают, что функция может быть и не определена в самой точке .

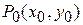Пример. Доказать, пользуясь определением предела по Коши, что .

Решение. Область определения данной функции D 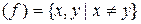. Выберем произвольное число 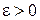и найдем 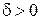, такое, что для любой точки 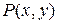, для которой справедливо 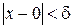, 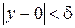выполняется неравенство 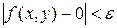. Так как для любой точки 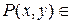D 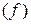справедливо соотношение

,

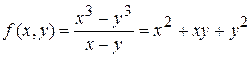то

.

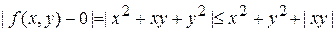Оценим :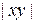

.

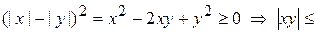
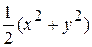Таким образом,

,

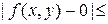
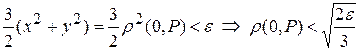где 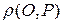— расстояние от точки 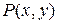до точки .

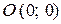Следовательно, для любого 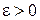мы нашли число 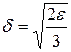, такое, что для любой точки 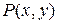, принадлежащей 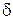-окрестности точки 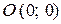, т.е. при 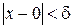, 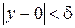будет выполняться неравенство

.

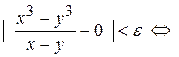
Что и требовалось доказать.

Приведенные выше определения предела функции двух переменных без труда обобщаются на случай функций трех и более переменных. Обобщим, например, определение предела по Коши на случай функции 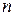независимых переменных.

Определение. Число А называется пределом функци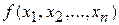и при 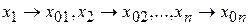,т.е. в точке 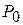, если для любого 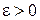существует 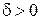, такое, что при всех 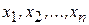, удовлетворяющих условиям | 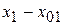| 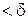, | | 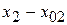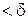,…, | | 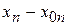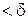, выполняется неравенство | 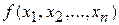— А| .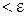

Пользуясь понятием предела функции, можно дать определение бесконечно малой функции при 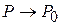( 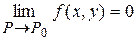), вывести основные свойства бесконечно малых функций, сравнить бесконечно малые функции, доказать теорему о том, что разность между функцией, имеющей предел, и ее пределом есть бесконечно малая функция, сформулировать основные теоремы об арифметических операциях над пределами. Все эти теоремы для случая 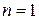были рассмотрены при изучении функций одной переменной.