Непрерывность функций нескольких переменных

Понятие непрерывности функции нескольких переменных можно определить с помощью предела.

Определение. Функция 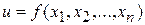называется непрерывной в точке 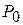, если выполнены следующие три условия:

1) 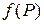определена в точке 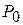и некоторой ее окрестности;

2) существует ;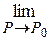

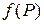3) = .

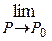
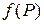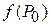Если в точке 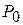одно из указанных трех условий не выполняется, то она является точкой разрыва функции .

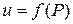Для функции 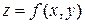двух независимых переменных точки разрыва могут быть изолированными или образовывать линию разрыва. Для функции 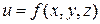трех независимых переменных точки разрыва могут быть изолированными, образовывать линию или поверхность разрыва.

Определение. Функция 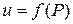называется непрерывной на множестве D, если она непрерывна в каждой точке этого множества.

Пример. Найти точки разрыва функции .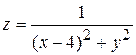

Решение. Данная функция определена на R² всюду, кроме точки 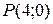, которая и является точкой разрыва функции.

Пример. Найти точки разрыва функции .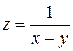

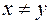Решение. Данная функция определена для любых , таких, что . Следовательно, прямая 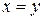является линией разрыва функции.

Пример. Найти точки разрыва функции .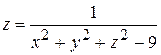

Решение. Функция 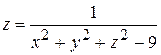определена для любых 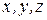, таких, что 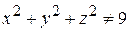. Следовательно, сфера с центром в начале координат и радиусом R=3 является поверхностью разрыва функции.