Уравнение парового объёма между клапаном и турбиной

Согласно принципу работы турбины и её схемы (рис.1) противодавление Р₂ очень мало по сравнению с давлением 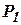и температурой 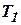изменяется незначительно. Поэтому можно принять:

.

(12.1)

Расход пара через клапан подсчитан по формуле Бендемана

,

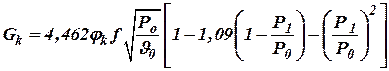(12.2)

где 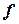- живое сечение клапана в м²;

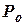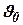, -начальное давление и удельный объем в кгс/м² и м³/кг;

- давление за клапаном в кгс/м²;

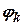- коэффициент расхода, определяющийся опытным путем.

Разность между расходом пара клапаном 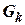и турбиной вызывает изменение удельного веса пара γ в рассматриваемом пространстве согласно уравнению

,

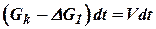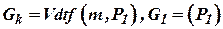
Расход 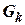зависит от величины подъема клапана, то есть от положения усилителя, определяемого координатой m, и от давления за клапаном 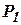(давление за клапаном полагают постоянным). Так как температуру за клапаном можно считать алгебраически связанной с давлением в паровом объеме 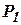, то расход является функцией только от 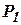. Поэтому для малых колебаний будут иметь силу уравнения:

,

(12.3)

.

(12.4)

Производные в (12.3) и (12.4) находятся путем дифференцирования (12.1) и (12.2)

.

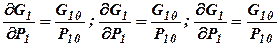Рисунок 12.2 – К вычислению частных производных

,

(12.5)

или графически (на основание характеристики клапанов)

При политропном состояния пара в паровом объёме ,

где – показатель политропа можно записать:

,

(12.6)

где ; ; ; ; .

После преобразования Лапласа уравнения парового объёма запишем:

,

(12.7)

или

,

Таким образом, паровой объём между клапаном и соплами в структурной схеме можно представить с перемещением звеном, передаточной функцией которого

.

(12.7)