Уравнение парового объёма за турбиной

где 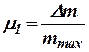- выход усилителя; 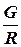- выход парового объёма;

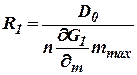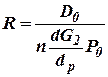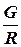; ; - характеризует саморегулирование.

В операторной форме уравнение (13.1) запишется как

,

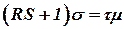(13.2)

где .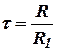

Для описания усилителей воспользуемся ранее полученными уравнениями:

,

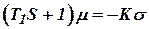(13.2)

Движение динамической системы в целом определяется системой дифференциальных уравнений (13.2) – (13.3), для которой получим характеристическое уравнение второй степени. Такая система обладает свойствами структурной схемы с двумя апериодическими звеньями.

Если изменения противодавления сравнительно слабо сказывается на расходе пара теплофикационными аппаратами, то 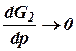, a 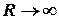. При этом в уравнении (13.1) член, характеризующий свойства саморегулирования 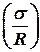турбины, становится пренебрежительно малым, тогда это уравнение можно записать так: 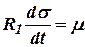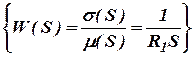_, - передаточная функция парового объёма.

При устранении свойств саморегулирования изменилась и структурная схема регулирования, т.к. паровой объём превращается из апериодического в интегрирующие звено .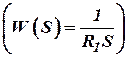

Отсюда следует:

1) Увеличение постоянной интегрирующего звена R₁ оказывает благоприятное влияние на процесс регулирования;

2) Увеличение веса пара, заключённого в камеры противодавления, оказывает благоприятное влияние на устойчивость и на процесс регулирования, т.к. паровой объём влияет такую же роль, как момент инерции ротора в конденсационной турбине.

3) Турбина с противодавлением – это динамическая система, в которой аккумулированный в камере пар играет положительную роль в процессе регулирования.