ПОГРЕШНОСТИ НАВИГАЦИОННЫХ ИЗОЛИНИЙ
Вероятнейший результат измерения навигационного параметра, исправленный поправками, -U, является обсервованным. Каждому обсервованному навигационному параметру соответствует своя навигационная изолиния или ее спрямленный (в районе счислимой или расчетной точки) участок - линия положения.
Из курса морской навигации известно, что линия положения характеризуется следующим уравнением (в нормальном виде):
∆φ cosτ + w sinτ = n (2.1.1)
Здесь ∆φ и w — поправки к координатам счислимой (расчетной) точки для получения обсервованного места (в минутах широты);
τ — направление градиента навигационного параметра относительно северной части географического меридиана;
n— перенос линии положения — кратчайшее расстояние между счислимой (расчетной) точкой С(рис. 2.1.1) и линией положения:
n = (U – Uс) / g (2.1.2)
где Uс— счислимый (расчетный) навигационный параметр, вычисленный относительно счислимой точки С;
g — модуль градиента навигационного параметра.
При наличии погрешности ∆U в обсёрвованном навигационном
параметре линия положения сместится параллельно самой себе на какую-то величину ∆n= ∆лп, т.е. изменится величина переноса. Величина смещения линии положения ∆лп обусловленная неточностью
навигационного параметра, называется погрешностью линии положения (навигационной изолинии). Для определения ее численного значения необходимо продифференцировать выражение (2.1.2) и перейти к конечным приращениям:

Рисунок 2.1.1.
∆n= ∆лп = ∆U / g (2.1.3)
Отсюда следует, что погрешность в линии положения зависит не только от величины ∆U,но и от градиента g:при данной погрешности ∆Uошибка в линии положения тем больше, чем меньше величина градиента. Но последняя зависит от положения корабля относительно ориентира, следовательно, градиент характеризует зависимость погрешности линии положения от геометрического фактора.
Значения градиентов различных навигационных параметров приведены в табл. 2.1.1.
Формулу (2.1.3) можно переписать так:
g = ∆U / ∆лп[ед. параметра/ед. длины] (2.1.4)
Отсюда видно, что модуль градиента навигационного параметра определяет изменение навигационного параметра при смещении линии положения по нормали на одну единицу длины.. Из этого определения следует простое правило расчета модуля градиента по карте с сеткой любых навигационных изолиний: разность значений двух соседних изолиний, между которыми находится место корабля — ∆, делится на расстояние между этими изолиниями L, т.е.
g = ∆ / L (2.1.5)
Средняя квадратическая погрешность линии положения определяется по правилу (2.3) после замены погрешностей на их средние квадратические значения:
σлп = σU / gили mлп = mU / g (2.1.6)
 Средняя квадратическая погрешность линии положения в отличие от погрешности навигационного параметра имеет направление — она перпендикулярна линии положения и поскольку равновероятен ее любой знак, то перпендикуляры равные σлп проводятся во взаимопротивоположные стороны (рис. 2.1.2) .
Средняя квадратическая погрешность линии положения в отличие от погрешности навигационного параметра имеет направление — она перпендикулярна линии положения и поскольку равновероятен ее любой знак, то перпендикуляры равные σлп проводятся во взаимопротивоположные стороны (рис. 2.1.2) .
Рисунок 2.1.2
Таблица 2.1.1.

Истинная (безошибочная) линия положения находится в полосе шириною 2σлпс вероятностью 0,683. При этом имеется в виду полоса, осью которой является обсервованная линия положения.
Ширина полосы, в которой находится безошибочная линия положения с заданной вероятностью Р, рассчитывается по формуле
Н = 2z σлп (2.1.7)
где z — вероятностный коэффициент, определяемый по табл. 1-б МТ-75. Линии положения являются равноточными, если одинаковыих средние квадратические погрешности. В противном случае они неравноточныи тогда им приписывается вес рлп:
рлп = 1 / σ2лп = g2 / σ2U (2.1.8)
Отсюда следует, что даже при равноточных навигационных параметрах линииположения в общем случае являются неравноточными из-за различия их градиентов.
Средняя квадратическая погрешностьσl положения по заданному направлению ll(см. рис. 2.1.2) называется векториальной.
Из треугольника оав
σl = σлп / sin α (2.1.9)
где а — угол междулинией положения и заданным направлением.
При α ≠ 90° σl всегда больше σлп т.е. средняя квадратическая погрешность линии положения является минимальной векториальной погрешностью.
Если рассматриваются две линии положения, пересекающиеся под углом Θ(рис. 2.1.3), то векториальные погрешности одной линии положения по направлению другой на основании формулы (2.1.9) будут равны
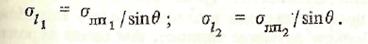 (2.1.10)
(2.1.10)

Рисунок 2.1.3
Проведя градиенты линий положения, можно вывести соотношение между углом Θ и углом между градиентами ∆τ:

 180° - ∆τ; ∆τ >90°;
180° - ∆τ; ∆τ >90°;
Θ =
∆τ; ∆τ ≤90°; (2.1.11)
На этом основании sin Θ = sin ∆τ и вместо выражения (2.10) можно написать
σl = σлп / sin∆τ (2.1.12)
Линии положения, соответствующие взаимозависимым навигационным параметрам, также взаимозависимы.
Дата добавления: 2015-08-14; просмотров: 1054;
