МАТЕМАТИЧЕСКИЕ МОДЕЛИ УСТАНОВИВШЕГОСЯ И ПЕРЕХОДНОГО РЕЖИМОВ И МЕТОДЫ ИХ ЛИНЕАРИЗАЦИИ
Напомним, что математическая модель установившегося режима (иначе — статическая характеристика элемента или системы) отражает функциональную связь между входными и выходными величинами в установившемся состоянии, а математическая модель переходного режима (динамическая характеристика элемента или системы) описывает изменение выходной величины во времени в зависимости от изменения входной величины.
Как уравнения статики, так и уравнения динамики могут быть линейными или нелинейными, в последнем случае они подлежат линеаризации.
|
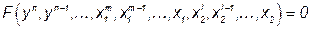 ,
,
где F — некоторая нелинейная функция; n, т, l — целые натуральные числа, определяющие наивысший порядок входящих в уравнение производных входной и выходной величин по времени.
Для реальных систем порядок дифференциального уравнения n > т и n > l. Линеаризацию нелинейных дифференциальных уравнений осуществляют методом малых отклонений. При этом вместо абсолютного значения переменных в уравнении (3.1) используют их отклонения от начального значения
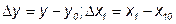 .
.
В результате уравнение (3.1) становится линейным ипри одной входной величине 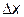 может быть записано в виде
может быть записано в виде
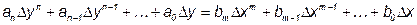 ,
,
где a0… an , b0… bm - постоянные коэффициенты.
Линеаризация уравнений статики.Уравнения статики элементов (систем) автоматического управления, как правило, нелинейные и могут быть представлены в виде кривой или ломаной линии.
Линеаризация нелинейных статических характеристик осуществляется несколькими способами.
Метод малых отклонений. Основан на разложении аналитической функции 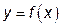 в ряд Тейлора и отбрасывании малозначащих членов.
в ряд Тейлора и отбрасывании малозначащих членов.
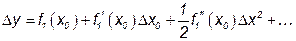
Таким образом, линеаризованное уравнение 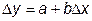 , где
, где 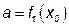 ;
; 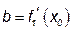 .
.
Метод касательной (рис. 3.1, а). Основан на замене участка кривой прямой линией, касательной к этой кривой в точке А (х0, у0), называемой рабочей точкой и находящейся в середине рабочего диапазона изменения 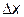 . Как и в предыдущем случае, линеаризованное уравнение
. Как и в предыдущем случае, линеаризованное уравнение 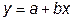 , где
, где 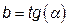 .
.
Метод секущей. Основан на замене уравнения нелинейной характеристики уравнением секущей, параметры которого определяют методом наименьших квадратов.
Первый из рассмотренных методов применяют, когда статическая характеристика задана аналитически, второй и третий — графически.
Встречаются элементы автоматической СУ, статические характеристики которых не поддаются линеаризации указанными ранее методами. Эти характеристики называют существенно нелинейными.
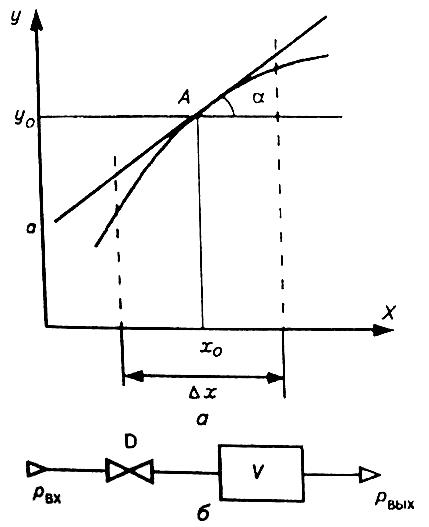
Рис. 3.1. Линеаризация статической характеристики (а) и модель пневматической камеры (б)
Дата добавления: 2015-07-14; просмотров: 2146;
