АНАЛИТИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Дифференциальные уравнения простых элементов можно составить, используя закономерности протекающих в них физических явлений. Такими закономерностями могут быть: закон сохранения вещества (объект регулирования уровня, давления), закон сохранения энергии (объект регулирования температуры), законы электротехники и т.д. Уравнения статических и переходных режимов составляют на базе уравнений балансов вещества или энергии.
При составлении дифференциальных уравнений сложного объекта (или системы) он должен быть расчленен на простейшие элементы, соединенные последовательно, для каждого из которых составляют математические модели статики и динамики. Дифференциальное уравнение объекта или системы в целом получают путем исключения промежуточных величин.
Как указывалось ранее, в большинстве случаев уравнения элементов нелинейные, и потому дифференциальное уравнение системы, как правило, нелинейное и подлежит линеаризации.
В целях упрощения задачи при использовании аналитического метода построения математической модели допускают определенные упрощения (пренебрегают распределенностью параметров, исключают несущественные возмущающие воздействия и т. д.).
Проиллюстрируем применение метода на примере пневматической системы (рис. 3.1, б), состоящей из дросселя D и камеры объемом V. Входная величина системы —давление рвх воздуха перед дросселем, выходная — давление рвых за камерой. Расход воздуха через дроссель 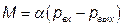 , где
, где 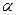 — коэффициент расхода (проводимость) дросселя, кг/(с • Па). С другой стороны, согласно уравнению состояния идеального газа
— коэффициент расхода (проводимость) дросселя, кг/(с • Па). С другой стороны, согласно уравнению состояния идеального газа 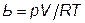 , где R — универсальная газовая постоянная; Т — температура газа, К. Изменение массового расхода за время
, где R — универсальная газовая постоянная; Т — температура газа, К. Изменение массового расхода за время 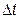
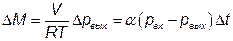 .
.
Разделив обе части уравнения на  , получим уравнение динамики элемента
, получим уравнение динамики элемента
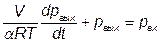 .
.
В статическом режиме 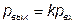
Чтобы получить такое простое уравнение, был сделан ряд допущений: процесс дросселирования газа считали изотермическим и не учитывали зависимость 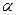 от
от 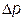 .
.
Дата добавления: 2015-07-14; просмотров: 2018;
