Основы обработки кинетических данных

Интегральные и дифференциальные методы нахождения констант скоростей и порядков реакций. Поиск констант скоростей линейным и нелинейным методом наименьших квадратов. Качественная и количественная оценка адекватности кинетических моделей экспериментов.

МНК. Линейная зависимость.

Рассмотрим реакцию первого порядка:

.

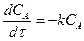В результате решения получается следующее уравнение:

.

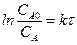Зависимость линейная, аналогична y = kx.

Любое нелинейное уравнение можно преобразовать в линейную форму вида:

y = b₀x₀ + b₁x₁,

где y – некоторая функция;

x – параметр процесса;

b – константы уравнения.

Если в уравнении только одна неизвестная константа скорости, то ее можно найти, используя выражение:

,

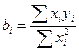тогда

y = b₁x₁.

Если две неизвестные константы, то:

.

,

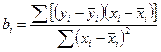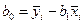где 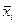- среднее значение.

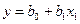
Суммирование производится по всем экспериментальным точкам.

Нелинейный метод наименьших квадратов применяется, если сложное кинетическое уравнение невозможно преобразовать в линейную форму.

При этом минимизируют сумму квадратов отклонений экспериментальных концентраций C_i и расчетных :

.

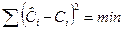Пример:

Дана реакция первого порядка

.

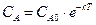
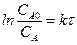Для какой-либо экспериментальной точки С_А находят значение k. По нему рассчитывают значение:

.

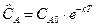Затем находят 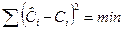и строят график:

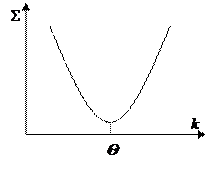
Θ – оптимальная константа скорости.

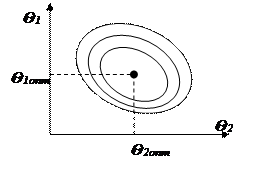
Если необходимо найти две константы скорости реакции, то действуют аналогично, находят значение Θ₁для k₁, фиксируют его. Находят Θ₂для k₂, фиксируют. Снова находят Θ₁, и повторяют до тех пор, пока не найдут оптимальные значения Θ₁ и Θ₂.