Общая постановка задачи упорядочивания.

В общем случае штраф от того, что заявка на решение i-ой задачи реализуется на к- месте в очереди, т.е. после решения предыдущих к-1 задач, могут быть произвольной функцией места в очереди, длительности ожидания или иных параметров и, в частности, затрат на настройку системы. Этот штраф может характеризовать некоторое значение коэффициента 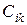,зависящего от типа задачи и очередности ее решения. Если значения штрафов 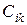взаимно независимы и суммарный штраф является минимальной функцией штрафов за решение i-ой задачи на к-ом месте, то задача оптимизации последовательности заявок может рассматриваться как задача минимизации линейного функционала:

.

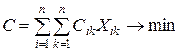Здесь 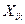=1, если i-ая заявка реализуется на к-ом месте и нулю в противном случае. Обычно заявки должны реализоваться без пропусков после завершения предыдущих подпрограмм и каждая заявка должна быть обязательна реализована. Это приводит к ограничениям:

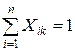
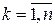
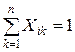
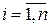
Подобным же образом задача составления оптимального расписания может быть сформулирована, если коэффициент 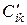характеризует величину выигрыша или дохода от реализации каждой i-ой заявки в k-ую очередь. При этом задача состоит в нахождении максимума линейной функции:

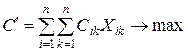, при тех же ограничениях.

Таким образом задача составления оптимального расписания реализации заявок может быть сформулирована как типичная задача линейного программирования – задача выбора или назначений. Точные методы решения задач такого вида весьма трудоемки, и при большой размерности имеются значительные технические и принципиальные трудности для получения технических решений. Однако, и при относительно невысокой размерности, типичной для составления оптимального расписания в ВС , точное решение задачи упорядочивания может требовать значительных затрат производительности. Быстрый рост обмена необходимых вычислений при увеличении размерности расписания приводит к появлению методов упорядочивания, перебора и ряда эвристических методов, позволяющих существенно сократить трудоемкость вычислений. Эти методы не всегда имеют строгое математическое обоснование и в некоторых случаях базируются на статистических экспериментальных оценках их точности. Качественно упростить получение первого приближения в задачах теории расписаний в их наиболее общей постановке можно следующими приемами:

1. ранжированием заявок, что позволяет заранее произвести их частичное упорядочивание и резко сокращает количество вариантов расписания;

2. введение промежуточных целей, когда оптимальное расписание составляется последовательно на интервалы времени. На эти интервалы разбивается все время планирования.

3. введением простейших функций штрафов.

Во многих случаях приемами ранжирования, промежуточных целей и упрощением функций 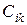пользуются интуитивно, не производя оценок отклонения значения функционала от его оптимального значения без введенных допущений. При этом приходится удовлетворяться тем, что полученные расписания лучше, чем неупорядоченные случайный выбор задач на реализацию.

Оценка качества упорядочивания при неполной информации о длительности исполнения работ и штрафах за ожидания или нарушения директивных сроков встречается с большими трудностями, и результаты, полученные в этой области аналитическими методами, весьма ограничены.