Принципы упорядочивания ресурсов ВС методами теории расписаний.

Алгоритмы распределения времени центрального процессора (ЦП) определяют последовательность выполнения программ. Эти алгоритмы по своей структуре могут быть классифицированы на приоритетные, бесприоритетные и смешанные.

В приоритетном алгоритме каждой программе присваивается приоритет выраженный целым числом k. Приоритет убывает с возрастанием k. Первой получает доступ к ЦП программа с высшим приоритетом. Программы с одинаковым приоритетом обрабатываются по алгоритму «раньше пришел - раньше обслужен» (РПРО). Существует два класса приоритетов: относительный и абсолютный. При относительных приоритетах появление новой программы с более высоким приоритетом не обрывает обрабатываемую программу, в отличие от абсолютных.

Кроме того, приоритеты подразделяются на статические и динамические. Если приоритет не изменяется с течением времени, он называется статическим, в противоположном случае – динамическим.

В бесприоритетных алгоритмах для каждой новой программы указывается правило постановки ее в очередь и задается предельное время (квант) ее первоначальной обработки (обслуживание). Формулируются также правила постановки в очередь или несколько очередей недообслуженных программ после каждого нового кванта обслуживания, который, вообще говоря, имеет различную продолжительность. Простейшим бесприоритетным алгоритмом является РПРО. Другим примером является круговой циклический алгоритм (КЦ). Здесь задачи обслуживаются фиксированными квантами времени, а недообслуженные программы ставятся в конец очереди (рисунок 3.1).

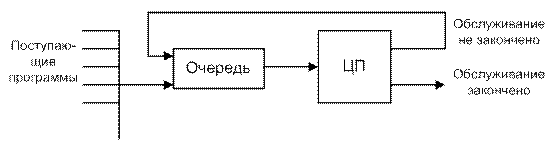
Рисунок 3.1.

По количеству очередей бесприоритетные алгоритмы делятся на одноуровневые и многоуровневые. Простейший многоуровневый алгоритм (ПМ) (рисунок 3.2) функционирует следующим образом. Организуется N очередей. Вновь поступающая заявка, занимает конец первой очереди. Первая программа из очереди с номером i > 1 поступает на обработку только в том случае, если очереди с номерами < i пусты. Программа с номером i<N обрабатывается в течение кванта времени, равного τ(i).

Незавершенная программа из очереди с номером N-1 попадает в конец очереди с номером N. Программа из очереди с номером N обслуживается по алгоритму РПРО, т.е. программы обрабатываются до конца без прерываний.

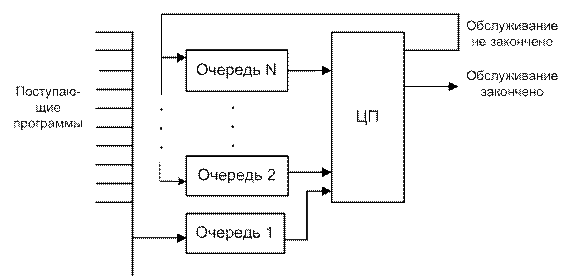
Рисунок 3.2.

Смешанные алгоритмы представляют собой сочетание приоритетных и бесприоритетных алгоритмов. Более того, программы с одинаковым приоритетом обслуживаются по одному из приоритетных алгоритмов. Новая программа с более высоким приоритетом, чем та, которая находится на обслуживании, получает доступ к ЦП сразу же после завершения обслуживания в текущем кванте. Введение приоритетов дает дополнительные возможности для ускорения обслуживания одних программ за счет замедления обслуживания других. Оптимизация пропускной способности ЦП достигается упорядочиванием программ по возрастанию процессорного времени. Это будет показано ниже. Вводятся относительные приоритеты 1, 2, … , k, при этом, чем меньше процессорное время обслуживания программы, тем выше ее приоритет. Если в ЭВМ постоянно поступают новые программы, то максимальную пропускную способность ЦП достигается при абсолютных приоритетах, назначенных по аналогичному правилу. В последнем случае приоритеты должны быть динамическими.

Учет ограничений на время ответа производится специальным образом. Время ответа измеряется с момента поступления программ на ЭВМ до момента завершения ее обработки (обслуживания) процессором. Иначе говоря, время ответа складывается из суммарного времени ожидания в очередях и времени обслуживания. Выполнение ограничений на время ответа особенно важно при работе ЭВМ в системе реального времени. В ряде случаев, когда основную загрузку ЭВМ составляют конечные совокупности программ, возникает задача нахождения порядка их обслуживания управляющим процессором с учетом ограничений на время ответа каждой программы.

Нарушение сроков обслуживания связано с определенными потерями. Необходимо найти приоритетный алгоритм, позволяющий обслуживать все программы без нарушения сроков обслуживания или с минимальными потерями.

Подобные задачи относят к теории расписаний. В вычислительных устройствах широкого назначения программы поступают на обработку в непредсказуемые моменты времени и требуют самых различных и заранее неизвестных затрат времени процессора. Какие-либо жесткие ограничения на время выполнения отдельных программ в таких системах не накладываются. В таких условиях используются равномерное распределение времени программ. Эффект такого распределения проявляется в том, что программа будет обрабатываться со скоростью обратно пропорциональной времени обслуживания и числу программ в очереди. Однако, реализация этого метода приводит к частым переключениям с одной программы на другую, что вызывает большие издержки ЦП. Поэтому при высокой загрузке ЭВМ короткими программами, программам с большим процессорным временем присваивают низкие приоритеты.

При известном времени обслуживания программы, можно вычислить отношение времени, проведенном в ЭВМ, ко времени обслуживания, которое называют относительной задержкой обслуживания. Система относительных динамических приоритетов, при которой следующей будет обслуживаться программа с максимальной относительной задержкой (МОЗ), представляет пример алгоритма распределения времени ЦП, приближающегося к равномерному. Такой алгоритм менее всего задерживает выполнение коротких программ, в то же время, эффективно ограничивает время ответа для программ с большим временем обслуживания.

Если есть информация о необходимом программе процессорном времени, то алгоритм должен перепланировать ЦП на программы с минимальным процессорным временем, как только она поступит. Такой алгоритм называется «наименьшее время - первый» (НМВП).

Как отмечалось, НМВП максимизирует пропускную способность. Однако, он обладает двумя недостатками. Во-первых, частые переключения ЦП с программы на программу приводят к значительным издержкам времени. Во-вторых, в отличие от алгоритма МОЗ, НМВП может сколь угодно долго задерживать выполнение длинных программ. Исходящая от пользователя информация о времени обслуживания часто бывает недостоверной, а иногда такую информацию невозможно получить. Поэтому возникла необходимость в разработке бесприоритетных алгоритмов, не опирающихся на какую-либо априорную информацию, и создающих по возможности меньшую задержку в обслуживании коротких программ. Алгоритм КЦ является простейшим удовлетворением этих требований. Реализация КЦ в чистом виде сопровождалась бы значительными затратами времени на переключение ЦП с программы на программу. Более гибким (в смысле минимальных затрат) является алгоритм простейший многоуровневый. Задачи аналитического исследования алгоритмического распределения времени ЦП являются задачами теории массового обслуживания.

В ряде случаев состав задач и длительность их решения можно считать известными и не зависящими от случайных факторов. Это позволяет рассматривать распределение ресурсов ВС как детерминированную задачу теории расписаний и решать методами этой теории. Основные математические модели и постановки задач в этом случае рассматриваются при следующих предположениях:

1. Все подлежащие выполнению работы полностью определены, т.е. известна последовательность времени поступления заявок и длительность решения каждой заявки.

2. Все заданные работы должны быть полностью выполнены, т.е. отсутствуют потери заявок.

3. Одна машина может одновременно решать только одну задачу, и не допускается прерывание до полного завершения реализации заявки.

В зависимости от характера потока заявок различают два вида задач теории расписаний: статические и динамические. В статических задачах предполагается, что все заявки, подлежащие упорядочиванию, поступают строго периодически, и расписание составляется каждый раз по всей совокупности заявок до полной его реализации. Формирование очередного пакета заявок происходит после обслуживания предыдущего пакета. Такой постановке задачи соответствует модель потока – однократное поступление всех заявок (пакет заявок).

В динамических задачах рассматриваются заявки, поступающие вне пакетов в некоторые априорно неизвестные моменты времени. В простейшем случае, предполагается, что поток – пуассоновский. Упорядочивание может производиться после завершения обслуживания каждой заявки, если за это время поступили новые. Трудоемкость упорядочивания после обслуживания каждой заявки делает целесообразным применение и анализ редкого упорядочивания после накопления нескольких заявок в очереди. Составление оптимальных расписаний может регламентироваться временем или случайным процессом полной реализации расписания, составленного для заявок, оказавшихся в очереди. Однако, во всех задачах сохраняется предположение об априорно известной длительной реализации каждой заявки.

Пусть

t_i – момент поступления i-ой заявки, который может совпадать для группы из n заявок или различаться для каждой заявки.

T_i – длительность обслуживания i-ой заявки.

D_i – директивный срок, то есть допустимая длительность промежутка времени от момента поступления до реализации, при превышении которой считается, что системе наносится некоторый ущерб.

α_i – штраф за единицу времени ожидания результатов после поступления i-ой заявки.

Часть параметров(t_i, T_i) может быть объективно измерена, а часть(D_i,α_i) назначается методом экспертных оценок заказчиком.

Наиболее часто используемые критерии эффективности упорядочения в теории расписания следующие:

· средняя длительность ожидания от момента поступления заявки до завершения ее обслуживания (средняя длительность пребывания);

· максимальная длительность ожидания результатов с момента поступления заявки;

· среднее время запаздывания завершения обслуживания заявки относительно директивного срока;

· максимальное запаздывание завершения обслуживания заявки относительно директивного срока;

· вероятность запаздывания относительно директивного срока;

· ущерб от ожидания или запаздывания заявок с учетом различной стоимости за ожидание различных заявок.

Кроме того, иногда анализируют среднее число ожидающих заявок в очереди, коэффициент использования системы и другие критерии. При перечисленных критериях целесообразно проводить обслуживание пачки заявок, поступивших одновременно, без прерываний и простоев. Доказано, что при этих условиях поиск оптимальных решений должен производиться в классе перестановочных расписаний. При такой постановке необходимо найти последовательность чисел t_i времени начала реализации i-ой заявки, при которой критерии качества принимают экстремальные значения.

В простейшем случае можно считать, что суммарный штраф за ожидание линейно зависит от запаздывания решения i-ой задачи и характеризуется коэффициентом штрафа α_i за единицу времени.

Тогда длительность ожидания до получения результата:

,

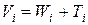где W_i - время ожидания в очереди до начала обслуживания.

Штраф за ожидание можно представить в виде:

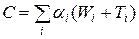
При этом важность и срочность задач характеризуется α_i. В ряде случаев важным является нарушение директивных сроков D_i решения каждой задачи, т.е. использование критериев своевременного выполнения работы. При такой постановке штраф определяется только по наибольшему или среднему нарушению директив срока i-ой задачи D_i.

Критерий качества при этом представляется следующей функцией:

,

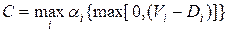где 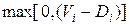- величина превышения директивного срока. Нарушение директивного срока может иметь место не только для отдельных задач, но и для реализации значительной части заявок. В этом случае используется критерий, учитывающий суммарный штраф за нарушение директивных сроков:

.

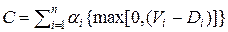При одновременном поступлении всех заявок оптимальный порядок в расписании будет в том случае, когда целевая функция является суммой штрафов за ожидание от моментов появления заявки до получения результата. Оптимальный порядок в расписании может быть получен методом динамического программирования на основе принципа Беллмана. При этом используется пошаговое конструирование расписания на основе принципа оптимальности любой части расписания, когда оно в целом оптимально.

Для суммы штрафов при оптимальной очередности обслуживания первых i заявок с длительностью решения для каждой заявки 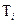уравнение Беллмана имеет вид:

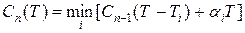(1)

Выражение (1) отражает тот факт, что при оптимальной последовательности решения всех n задач за полное время Т, последовательность решения n-1 задач за время Т-T_i должна быть также оптимальной. Минимум суммы штрафов достигается в оптимальной последовательности, когда перестановка обслуживания любых двух, в том числе и последних заявок, не может уменьшить сумму штрафов.

Раскрывая значения штрафов для двух последних заявок можно записать: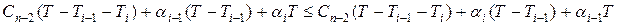

Отсюда получаем:

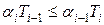или

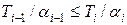(2).

Это означает, что оптимальное расписание следует составлять по решающему правилу (2), то есть в порядке неубывания отношения длительности обслуживания к штрафам за единицу времени ожидания.

Если α_i=1 , то расписание соответствует упорядочиванию по неубывающим значениям . В теории расписаний доказывается, что при таком упорядочивании минимизируется среднее число заявок в системе и средняя длительность ожидания до начала реализации заявок.

Аналогично предыдущему с использованием уравнения Беллмана может быть получено решающее правило для расписаний при критерии нарушения директивных сроков. Для оптимизации последовательности решения задач минимальное и максимальное отклонения должны выполняться и для двух последних задач. Если изменить порядок решения двух последних задач, то значение функционала не станет меньше, так как полученный порядок является по построению оптимальным.

В качестве последней задачи, подлежащей решению, в расписании следует выбрать ту, для которой выполняется:

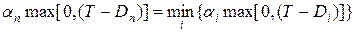
В качестве предпоследней выбирается задача, для которой выполняется

условие:

.

Если при одновременном поступлении всех заявок существует такое упорядочивание, которое обеспечивает полное отсутствие нарушения директивных сроков, то по правилу (2) заявки могут быть упорядочены так, чтобы значение средней длительности ожидания до завершения обслуживания и получения результатов было минимальным. Это означает, что последняя реализуемая заявка, которая не нарушает директивного срока и характеризуется максимальной длительностью реализации среди всех заявок, выполнение которых в последнюю очередь не приводит к нарушению директивных сроков.

Построение оптимального расписания в этом случае можно производить рекуррентно, начиная с последней заявки. Из всех совокупностей заявок выбираются те, для которых директивные сроки превышают суммарную длительность выполнения всех работ 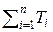. Из заявок, удовлетворяющих этому условию, отбирается одна с наибольшей длительностью использования и закрепления на последнем месте. Далее, рассчитывается суммарное время реализации n-1 заявки, с которым сравниваются директивные сроки оставшихся заявок, и повторяется выбор предпоследней заявки и т.д.

Для общего случая, когда не существует расписания, обеспечивающего выполнение всех директивных сроков и, кроме того, директивные сроки нарушаются не для всех заявок, разработан ряд эвристических алгоритмов.

Предварительное упорядочивание по не убыванию значения 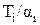и последующие перестановки с целью сокращения нарушений директивных сроков приводят во многих случаях к достаточно удовлетворительным результатам.

Для случая неодновременного поступления заявок в настоящее время не получены простые решающие правила при достижении общих условий с директивными сроками. При этом возникает проблема получения правила выбора оптимального интервала времени корректирования расписания с учетом того, что изменение расписания при появлении любой новой заявки может оказаться сопряженным с большими затратами на его оптимизацию. При неодновременном поступлении заявок и учете затрат на составление оптимальных расписаний оценку эффективности дисциплин приходится в основном производить методом статического моделирования.