Оптимизация распределения памяти по иерархическим уровням.
В современных ВС широко используются запоминающие устройства (ЗУ) различных типов. ЗУ различаются физическими принципами, а, главное, техническими и экономическими параметрами. Основными параметры ЗУ являются:
· Время обращения к ЗУ (длительность поиска + перепись данных).
· Стоимость устройства, обеспечивающего хранение 1 единицы информации (1 бита).
· Объем информации, хранимой в ЗУ.
Важнейшим фактором, характеризующим ВС, является их производительность, которая в значительной степени зависит от быстродействия запоминающих устройств.
Однако, ЗУ с большим быстродействием имеет большую стоимость. Эти обстоятельства явились определяющими для выдвижения концепции многоуровневой иерархической памяти, широко используемой в современных ВС.
Использование многоуровневой памяти позволяет существенно снизить стоимость хранения больших объемов информации при некотором допустимом снижении быстродействия ВС. Для устройства памяти, непосредственно взаимодействующего с процессором, используются самые дорогие и быстродействующие ЗУ. Следующее устройство памяти с меньшим быстродействием и большим объемом непосредственно не связано с процессором и снабжает данными память высшего уровня. Таким образом, создается иерархическая многоуровневая память, в которой ЗУ располагается в порядке убывания быстродействия и стоимости хранения единицы информации и, соответственно, в порядке возрастания объема хранимых данных. Отсюда можно сделать вывод, что первая задача, которая возникает при анализе эффективности многоуровневой памяти, состоит в исследовании методов оптимального построения иерархической памяти, методов распределения типов памяти и их объемов, обеспечивающих экстремальное значение некоторого критерия эффективности.
Стоимость оптимизации многоуровневой памяти позволяет получить конструктивные решения только при ряде упрощений и приближений в описании функционирования реальных систем, основанных на исследовании обмена информацией между ЗУ различных типов.
Выбор типов данных и программ, их объема и порядка перемещения между уровнями памяти во многом определяет реальное быстродействие ВС.
Анализ эффективности использования многоуровневой памяти предполагает решение следующих задач:
· Разработка методов оптимального построения иерархической памяти и распределения типов памяти по различным уровням.
· Разработка методов оптимальных дисциплин обмена данными в зависимости от типов памяти.
· Оптимизация алгоритмов обработки информации и массивов данных с целью повышения эффективности функционирования ВС с многоуровневой памятью.
При решении этих задач вводятся упрощающие предположения и учитываются только важнейшие характеристики.
При обмене данными широко используются страничная организация памяти. При этом функциями системы динамического распределения памяти являются: размещение информации в виртуальной памяти, текущее отображение виртуальной памяти на физическую (распределение информации по различным уровням памяти), управление обменом информации между уровнями памяти.
Доминирующим фактором при построении критериев оценки многоуровневой памяти являются производительность ВС. Вторым показателем качества является стоимость памяти. Это определило наиболее широкое использование схем оптимизации памяти с использованием показателей «производительность – стоимость». При этом наиболее часто используется следующие два основных критерия: стоимость памяти при заданной производительности ВС и производительность ВС при заданной стоимости памяти. Остальные критерии, так или иначе, связаны с названными.Задача оптимизации памяти является сложной задачей (недостоверная информация, большое количество факторов, размерность и т.д.). Поэтому анализ многоуровневой памяти ведется путем анализа сложных систем: путем декомпозиции полной задачи оптимизации на ряд частных задач.
Эта декомпозиция сводится к следующим группам задач:
· Распределение памяти по уровням иерархии.
· Динамика вызова и замещения массивов данных (страниц) в ОП.
· Анализ режима взаимодействия с внешней памятью.
Одна из задач использования многоуровневой памяти состоит в оптимальном выборе объемов памяти различных типов, при котором либо среднее время обращения при заданной стоимости ВС минимально, либо стоимость ВС при заданном среднем времени обращения минимальна. При этом предполагается, что компоненты памяти известны и различаются временем выборки и стоимостью хранения единицы информации, а также объемом памяти. Для оптимизации необходимо задать объем памяти, а также «активность» программ или частоту вызова их на решение.
Задача рассматривается при следующих предположениях:
· общий объем памяти комплекса программ состоит из совокупностей подпрограмм, каждая из которых занимает одинаковый объем памяти (блок).
· Подпрограммы объединяются в M групп по Wi блоков, вызываемых с частотой Fi. Вводится понятие активности i-ой группы использования подпрограмм:
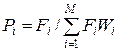 ,
,
при естественном ограничении:
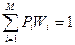 .
.
Таким образом, i-ая группа подпрограмм характеризуется объемом занимаемой памяти Wi и активностью обращения к ней Pi, которые могут быть либо рассчитаны аналитически, либо определены моделированием или экспериментально. Иерархическая система ЗУ состоит из N компонент, каждая из которой описывается двумя параметрами: временем обращения к одному блоку Тк и затратами (стоимостью хранения) на блок Ск. На нижнем уровне располагается массовое устройство: ЗУ с минимальной стоимостью хранения одного блока и объемом, достаточным для хранения всего комплекса программ и массивов данных.
Это ЗУ характеризуется суммарной стоимостью Go, а полная стоимость памятей всех типов равна G. При таком ограничении ставится задача минимума среднего времени обращения к любому массиву информации или программе.
В ЗУ k-ого типа расположены Vik блоков программ с активностью Pi, таким образом, для группы программ с такой активностью выполняется условие:
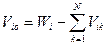
Общая стоимость хранения в ЗУ N типов блоков с М уровнями активности равна:
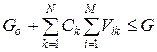
При этом должны выполняться следующие ограничения:
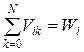
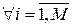
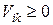
Задача состоит в минимизации среднего времени обращения к блоку:
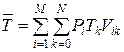
путем варьирования блоков в ЗУ каждого типа.
Если ЗУ упорядочены так образом, что С3>С2>С1 и T3<T2<T1 , а также выполняется условие:
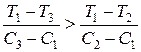 ,
,
то можно доказать, что использование ЗУ типа 2 приводит к улучшению характеристик системы. При этих условиях характеристики ЗУ типа 1 и 3 доминируют над характеристиками типа 2. Это положение позволяет выделить совокупность тех типов ЗУ, которые целесообразно применять в системе. Для этого первоначально определяется тип ЗУ, имеющий максимальное изменение времени выборки на единицу затрат относительно ЗУ нулевого типа:
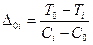
Все ЗУ, упорядоченные по не возрастанию Tj (то есть по убыванию) и имеющие номера в пределах 0<j<i могут быть исключены из рассмотрения как не увеличивающие эффективность системы. Далее, в пределах старших номеров ЗУ i<l<N определяется l-ый номер ЗУ, для которого максимальное изменение длительности обращения на единицу затрат равно:
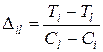
Таким образом, последовательно выбираются все типы ЗУ, которые по своим характеристикам приращения времени обращения на единицу затрат доминируют над остальными и нумеруется от 0 до n.
Затем, можно рассчитать среднее время обращения и определить оптимальные объемы ЗУ различных типов. Эти расчеты начинаются с определения приоритетов обмена с учетом активности, которая характеризуется величиной:
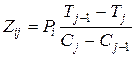
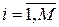
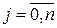
Значения Zij-упорядочены по убыванию, это обеспечивает первоочередную выборку блоков с максимальным приращением среднего времени обращения на единицу затрат с учетом активности. Передача, связанная с приоритетом Zij представляет собой перенос программ характеризующихся активностью Pi из ЗУ j-1 в ЗУ типа j. При этом необходимо исключить Wi блоков из ЗУ (j-1) типа и увеличить на ту же величину объем ЗУ j-ого типа, что приводит к увеличению затрат на величину:
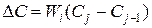
Изменение среднего времени обращения равно:

В качестве начального состояния целесообразно рассмотреть размещение всей информации в ЗУ нулевого типа, что обеспечивает минимальные затраты G0 и время обращения T0. Выполнив последовательно передачи групп блоков программ и данных Wk на более высокие уровни памяти с соответствующим увеличением затрат на величину 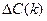 , можно построить график суммарных затрат:
, можно построить график суммарных затрат:
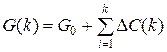 ,
,
и определить номер передачи k, являющийся предельным при заданном ограничении на суммарную стоимость памяти. Одновременно могут быть рассчитаны приращения среднего времени обращения:
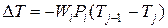 ,
,
а также, сумма этих величин в зависимости от k и среднее время обращения к памяти:
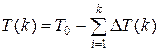
Дата добавления: 2015-08-14; просмотров: 1079;
