Модели поведения программ и критерии качества.

Для сравнения различных алгоритмов замещения необходимо указать способ задания последовательности обращений 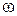. Простейший способ заключается в задании фиксированной последовательности обращений 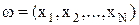, которые получаются путем записи по ходу выполнения программы последовательности обращений к ее страницам. Вся последовательность обращений предполагается заранее известной. Модель поведения программы, соответствующей этому способу задания 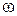, называется детерминированной. В рамках детерминированной модели алгоритмы замещения сравниваются на каждой последовательности обращений в отдельности, и для получения достоверных результатов сравнения требуется набрать достаточное количество последовательностей обращений. При этом, возникает вопрос, насколько представлена имеющаяся выборка последовательностей обращений. Трудности оценки представительности выборки, большие затраты машинного времени на генерацию последовательности привели к появлению стохастических моделей.

Простейшая стохастическая модель (независимая модель) описывает обращения x₁,x₂,… последовательностью независимых (одинаково распределенных) случайных величин:

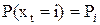
Непосредственным обобщением такой независимой модели является марковская модель, которая описывает обращения x₁,x₂,… однородной эргодической цепью Маркова 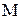, заданной на множестве состояний 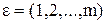матрицей переходных вероятностей:

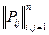, где

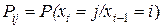
Выделим частную марковскую модель со специальной переходной матрицей с элементами:

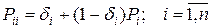
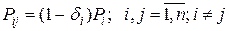
Где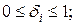

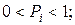
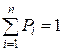
Такая модель интерпретируется следующим образом. В начальный момент времени из множества 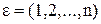выбирается независимым образом страница 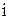в соответствии с распределением 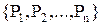. Последующие 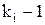обращения происходят также к этой странице, причем 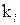подчиняется геометрическому распределению:

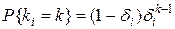
То есть очередное обращение к странице 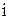происходит с вероятностью 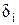. После 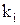обращений к странице 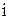следующая страница выбирается независимым образом из множества 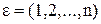в соответствии с вероятностным распределением 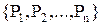и т.д. Распределение 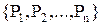и вероятность 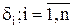являются параметрами частной марковской модели.

Обобщение частной марковской модели на случай произвольного распределения величины 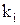приводит к полумарковской модели поведения программ.

Независимая модель с непрерывным временем задается посредством совмещения 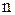независимых пуассоновских процессов с интенсивностью 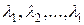. Пуассоновский процесс с интенсивностью 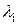определяет поток сообщений к странице 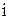, причем 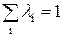, следовательно, интенсивность 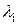соответствует вероятности обращения к странице 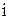. В этой модели интервалы между двумя соседними обращениями к одной и той же странице имеют экспоненциальное распределение. В общем случае, заменяя экспоненциальное распределение на произвольное, получаем модель, которая называется моделью восстановления.

Модель восстановления задана, если:

а) имеется 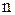функций распределения 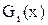, описывающих 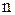независимых случайных величин и 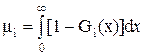существует.

б) интервалы между соседними обращениями к странице 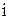независимы и подчиняются распределению .

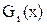в) выполняется условие нормировки: .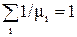

Так как 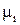- среднее время между соседними обращениями, то последнее условие означает, что в среднем в единицу времени происходит одно обращение к одной из страниц программы.

Критерии качества.

Так как алгоритм замещения влияет прежде всего на частоту страничных сбоев, то эта величина должна определять критерий качества.

Определим для любого 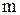- элементного подмножества 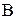характеристическую функцию его дополнения:

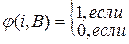
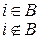
Для детерминированной модели критерий качества определяет количество обращений к ВП при применении алгоритма замещения 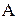на последовательности обращений 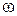длины :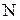

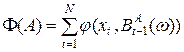
Для всех рассмотренных выше стохастических моделей критерий качества зададим в виде:

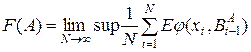
Такой критерий качества определяет среднюю стационарную частоту обращений к ВП или, иначе говоря, среднюю частоту страничных сбоев.

Адекватность модели.

Для любой стохастической модели поведения программ возникает вопрос,

насколько хорошо, она описывает трассы обращений реальных программ, т.е. вопрос об адекватности модели. Вводится понятие адекватности в сильном, широком и слабом смысле.

Модель адекватна в сильном смысле, если для рассматриваемой последовательности обращений реальной программы с заданной статистической достоверностью выполняются предположения, определяющие исходную модель. Для практических приложений адекватность в сильном смысле обычно не требуется. Вполне достаточно близости значений некоторых функционалов, определяемых по модели и по последовательности обращений реальной программы. Отсюда возникает понятие адекватности в широком смысле. Модель адекватна в широком смысле, если значения заданного функционала, полученные по модели и по реальной трассе обращений близки (по заданному критерию близости).

При сравнении алгоритмов замещения значительный интерес представляет также модели, отражающие только отдельные свойства реальных трасс обращений. К таким свойствам, прежде всего, относятся свойства рабочего тела, локальности и редких обращений.

Свойство рабочего тела заключается в том, что существует сравнительно небольшое подмножество страниц программы (зависящие от времени) при вводе которых в ОП частота страничных сбоев резко падает.

Свойство локальности заключается в том, что происходит много обращений подряд к относительно небольшим подмножествам страниц программы.

Свойство редких обращений заключается в том, что, несмотря на наличие рабочего тела, и отрезка локальности, в последовательности обращений встречаются редко используемые страницы.

Модель адекватна в слабом смысле, если она отражает указанные три свойства: рабочего тела, локальности и редких обращений.

Все рассматриваемые стохастические модели адекватны в слабом смысле, то есть частная марковская и простейшая полумарковская модели отражают простейший вид локальности, когда несколько обращений подряд происходит к одной странице.

С точки зрения сравнения алгоритмов, можно показать, что:

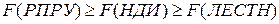
При этом:

;

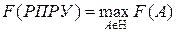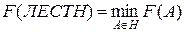
Таким образом, алгоритм замещения ЛЕСТН является оптимальным алгоритмом в классе 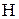для модели независимых обращений.