Формула Шихмана
Часто применяют неявную формулу Шихмана 2 – го порядка.
Xk+1=( - 1/3) Xk-1+ (4/3) Xk+(2/3) h F(Xk+1, tk+1),
Здесь b1=2/3, b2=1/3. По формуле: Xk+1= Xk +(2/3) h F(Xk+1, tk+1) +(1/3) h F(Xk),
Заменяя производную F(Xk)=(Xk - Xk-1)/ h, получим искомую формулу.
Неявные методы удобно применять для алгебраизации дифференциальных уравнений, заменяя производные формулами неявных методов.
Например
Ψ(∂Х/∂t , X, t) = 0.
Заменимпроизводную по формуле Шихмана, получим:
Ψ(1/ h[( 3/2) Xk+1+ (1/2)Xk-1 - 2Xk)], Xk+1, tk+1) = 0.
Эта алгебраическая система решается численными методами относительно Xk+1.
Полученные формулы для производных являются частными случаями общей формулы неявных методов Гира.
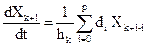 .
.
p = 1- формула Эйлера, d1=1; p = 2 – формула Шихмана, d1=4/3; d2=-1/3.
Формулы Гира называют также формулами дифференцирования назад (ФДН).
Дата добавления: 2015-08-14; просмотров: 1012;
