Метод Ньютона

Система нелинейных уравнений может быть записана виде:

F(X) = 0

f₁(x) = 0

f₂(x) = 0

………..

f_n(x) = 0

Х = (х₁; х₂; …; х_n)

Мы линеаризируем эту функцию в точке Х_к-1 , т.е. приведем к линейному виду.

Для этого раскладываем в ряд Тейлора.

,

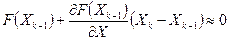
где X_k= X_k-1+ ∆X_k .

∂F₁/∂X₁; ∂F₁/∂X₂; ….∂F₁/ ∂X_n

∂F₂/∂X₁; ∂F₂/∂X₂;….∂F₂/∂X_n;

∂F/∂X = ………………………………… – матрица первых производных.

∂Fn/∂X₁; ∂F/∂X_n;…..∂F/∂X_n

Итерационный процесс заканчивается, когда ║∆X_k ║≤ ε₁

║ F(X_k ) ║≤ ε_2,

где норма вектора отождествляется с его длиной:

║А║ = √ А₁² + А₂² + …. +А_n²,

А= (А₁, А₂, …А_n)

Недостатком метода является то, что не всегда имеет место сходимость решения. Если имеется сходимость, то она носит квадратичный характер, т.е.

║Х_к – Х_к-1║²≤║Х_к – Х^*║,

где Х^* - точное решение.

Для линейной системы уравнений решение находится за одну итерацию.

Метод Ньютона – Рафсона ( метод продолжения решения по параметру)

Решение ищется, начиная с известного решения для кого-то значения параметра (которое принимается за начальное), и постепенно по шагам приближаясь к заданному значению. В электрических цепях за такое начальное решение принимается тривиальное решение для переменных (токов и напряжений) равное нулю при равенстве нулю всех источников в цепи.

,

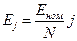где j = 1, 2, …N. При j = 1 принимаем E=0 и постепенно его значение увеличиваем.