Метод Гаусса с выбором главного элемента

Метод Гаусса относится к точным методам решения. Если исключить погрешности округления при вычислениях (использовать обыкновенные дроби), то за конечное число операций можно получить точное решение.

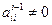Анализ алгоритма решения показывает, что точность определяется значениями коэффициентов, расположенных на главной диагонали , которые называют ведущимиэлементами. На каждом шаге прямого хода предполагалось, что .Если это не так, то в качестве ведущего элемента можно использовать любой другой ненулевой коэффициент поменяв местами строки или столбцы матрицы. Однако если он окажется малым то после деления на этот элемент и последующего вычитания возникают большие погрешности округления. Чтобы избежать этого, на каждом этапе строки и столбцы переставляют так, чтобы наглавной диагонали оказался наибольший по модулю элемент. Поскольку одновременный перебор строк и столбцов увеличивает количество операций и усложняет алгоритм, то обычно перебирают только строки. Найденный элемент, наибольший по модулю называют главным. В этом состоит суть метода Гаусса с выбором главного элемента.

Метод имеет малые погрешности округления при условии если матрица системы хорошо обусловлена. Матрица называется плохо обусловленной, если Алые изменения её элементов приводят к существенным изменеиям элементов обратной матрицы 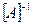. Произведение ведущих элементов равно определителю системы:

.

Откуда следует, что если система имеет решение - 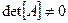, то всегда можно найти ведущие элементы отличные от нуля и, следовательно, найти решение методом Гаусса с выбором главного элемента.

Метод Гаусса с выбором главного элемента надежен, прост и наиболее выгоден для систем ЛАУ с плотно заполненной матрицей.