Постулаты Бора. Атом водорода по Бору.

Классическая теория не могла объяснить ни устойчивость атома, ни характер атомного спектра. Выход из создавшегося тупика был найден в 1913 г. датским ученым Нильсом Бором, правда, ценой введения ряда предположений (постулатов), противоречащих классическим представлениям.

I постулат (постулат о стационарных орбитах).

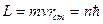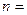Из множества возможных с точки зрения классической механики электронных орбит в атоме реализуются лишь некоторые дискретные, так называемые стационарные орбиты. На стационарных орбитах момент импульса электрона имеет квантованные (дискретные) значения , где 1, 2, 3, …- квантовое число, 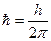- постоянная Планка. Электрон, двигаясь по стационарным орбитам не излучает электромагнитных волн.

I постулат позволил Бору сделать атом устойчивым.

Исходя из I постулата, можно рассчитать радиусы стационарных орбит. Действительно, исходя из уравнения движения и I постулата Бора, выполнив некоторые преобразования, получим:

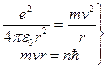следовательно, ,

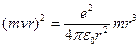откуда

.

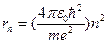Тогда 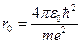= 0,5 А – первая боровская орбита, соответствующая наиболее устойчивому состоянию электрона в атоме водорода.

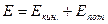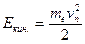Исходя из закона сохранения энергии , где , а 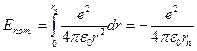и I постулата Бора 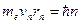, можно рассчитать энергию атомов в различных состояниях:

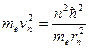, а 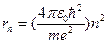, тогда .

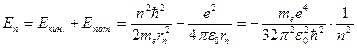II постулат (условие частот Бора).

Атом излучает (поглощает) энергию только при переходе электрона с одной стационарной орбиты на другую. При этом излучение (поглощение) света происходит в виде квантов света с энергией 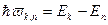, где 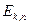- энергия электрона на стационарной орбите.

Существование дискретных энергетических уровней атома было экспериментально подтверждено в 1914 г. Франком и Герцем, наблюдавшими протекание тока в трубке с парами ртути. Когда электроны, испущенные катодом, приобретали под действием внешнего ускоряющего поля энергию, кратную величине 4,9 эВ, ток в цепи резко падал (рис.4). Этот результат объясняется тем, что вследствие дискретности энергетических уровней атомы ртути могут воспринимать энергию только порциями 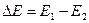=4,9 эВ. Пока энергия ускоренных электронов, вылетевших из катода, меньше 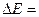4.9 эВ, соударения между электронами и атомами ртути носят упругий характер. При энергиях электронов 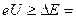4,9 эВ их соударения с атомами становятся неупругими, поэтому электроны, потерявшие энергию вследствие столкновений, не могут преодолеть небольшой задерживающий потенциал между сеткой и анодом: ток в цепи резко падает. При 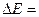9,8 эВ электроны сильно теряют энергию после двух столкновений и т.д. Когда пары ртути достаточно разрежены, то электроны до столкновения успевают набрать энергию 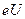= 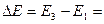6,7 эВ. При этом на зависимости I(U) появляется спад тока в области 6,7 В.

II постулат Бора позволил объяснить спектральные закономерности излучения водородоподобных атомов.

Атом водорода по Бору представляет собой систему, состоящую из положительно заряженного ядра, в котором сосредоточена практически вся масса атома, и электрона, вращающегося вокруг ядра по стационарным орбитам ( 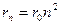) (рис.3).

Согласно II постулату Бора

,

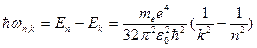откуда

.

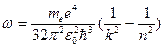Таким образом, мы получили сериальную формулу Бальмера-Ридберга, где 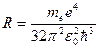(в системе СГС 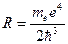) - постоянная Ридберга.

Чтобы получить спектр излучения атомов, например, атомов водорода, необходимо привести их в возбужденное состояние, т.е. перевести электрон с уровня 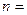1 на уровень с более высоким 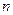. Это можно сделать путем бомбардировки атомов пучком электронов, ускоренных до определенных энергий в электрическом поле. В зависимости от энергии электронного пучка можно добиться последовательного возбуждения атома вплоть до ионизации. В спектре излучения возбужденных таким образом атомов наблюдается последовательное появление линий излучения, связанное с энергией электронного пучка (начиная с первой линии серии Лаймана). Такое появление линий излучения в спектре водорода легко объясняется с точки зрения теории Бора и не может быть объяснено с точки зрения классической теории, в соответствии с которой весь спектр должен был бы появиться одновременно.

Таким образом, модель Бора успешно объяснила закономерности атомных спектров водорода и водородоподобных ионов (т.е. ионов с одним внешним электроном, например, 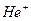, 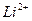). Если ядро такого иона имеет заряд 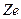, то радиус стационарных орбит определяется выражением 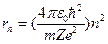(в системе СГС 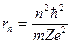), энергия иона 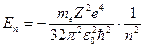(в системе СГС 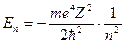), сериальная формула 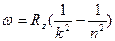, где .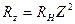

По представлениям теории Бора электрон в атоме водорода движется по стационарной орбите. С этим связан орбитальный механический момент атома 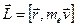(см. рис.). Кроме того, с движением электрона связан кольцевой ток 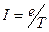( 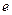- заряд электрона, 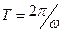- период обращения электрона вокруг ядра), а, следовательно, и магнитный момент атома

,

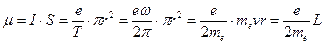или в векторной форме

.

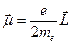Отношение магнитного и механического моментов называется орбитальным гиромагнитным отношением

.

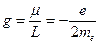Это отношение играет большую роль в атомной физике. Мы вернемся к нему при изучении квантовой физики атомов. Из теории Бора 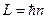. Следовательно

,

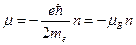где 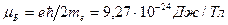- это величина, называемая магнетоном Бора.

Теория Бора, отличавшаяся смелостью и простотой, дала ответы на многие вопросы, волновавшие физиков-экспериментаторов того времени, но наряду с этим не позволила решить целый ряд проблем, т.к. обладала существенными недостатками:

- теория внутренне противоречива, т.к. в ней классические представления дополнены постулатами, противоречащими классической физике;

- теория не объясняет закономерностей многоэлектронных систем: структуры и спектров атомов более сложных, чем атом водорода;

- теория Бора не дает полного описания даже атома водорода: давая правильно значения частот спектральных линий, она не позволяет вычислять их интенсивность и конечную ширину;

- из теории Бора вытекает, что атомы имеют осевую симметрию, но данные по структуре кристаллов свидетельствуют о том, что форма атомов ближе к сферической.

Квантово-механическое представление атома водорода.

Гипотеза де Бройля. Электромагнитное излучение (свет) обладает одновременно и волновыми и корпускулярными свойствами. В этом проявляется корпускулярно-волновой дуализм.

В 1924 г. Луи де Бройль выдвинул смелую гипотезу, что корпускулярно-волновой дуализм является особенностью не только электромагнитного излучения, но имеет универсальное значение. Он предположил, что любая микрочастица (а не только фотон) обладает корпускулярно-волновыми свойствами. Более того, де Бройль предположил, что связь между характеристиками микрочастицы как волны, так и корпускулы, такая же, как и у фотона. Для фотона, например, импульс (характеристика частицы) связан с длиной волны (характеристикой волны) соотношением

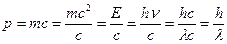, откуда .

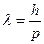Согласно де Бройлю, любая микрочастица может характеризоваться длиной волны 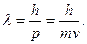Оценим, например, величину 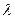для электрона, ускоренного полем с разностью потенциалов 25 В:

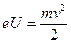, откуда 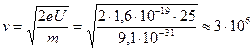м/с;

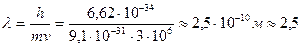Å,

т.е. такому электрону соответствует диапазон рентгеновских волн.

Если электроны действительно обладают волновыми свойствами, то они, согласно де Бройлю, должны вести себя подобно рентгеновским лучам. На этом основаны эксперименты, подтверждающие гипотезу де Бройля.

Характерным проявлением волновых свойств рентгеновских лучей является их дифракция на кристаллической решетке (т.к. постоянная решетки сопоставима с длиной волны). Для дифракции рентгеновских лучей справедлива формула Вульфа-Бреггов 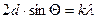- условие максимумов дифракционной картины (лучи, отраженные от одной плоскости решетки, усиливают лучи, отраженные от другой плоскости). Следовательно, и электроны должны дифрагировать на кристаллической решетке. Установили это экспериментально в 1927 г. К.Дж.Дэвиссон и Л.Х.Джермер. Схема одного из экспериментов была следующей (рис.6). В опыте угол 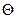выбирался постоянным, а длина волны менялась путем изменения ускоряющей разности потенциалов. Т.к. 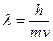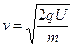, а , то 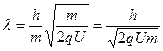. Условие максимумов: 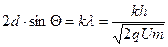, где 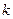= 1, 2, 3, … Отсюда максимум интенсивности регистрации электронов должен наблюдаться при 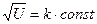. Экспериментальная зависимость подтвердила наличие волновых свойств у электронов, т.е. подтвердила гипотезу де Бройля.

Уравнение Шредингера. Квантовые числа.

Волновой процесс, соответствующий состоянию микрообъекта, может быть описан плоской монохроматической волной де Бройля только в случае свободного движения частицы, обладающей определенной энергией 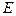и импульсом 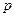. Функция, которая описывает волновой процесс в общем случае (произвольное движение частицы в произвольных полях), является весьма сложной. Она зависит от координат и времени, и называется волновой функцией или пси-функцией - .

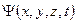Водородоподобные атомы представляют собой системы, состоящие из ядра, заряд которого 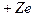и одного электрона (заряд 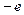). Примерами подобных систем являются атомы водорода Н, дейтерия D, трития T, ионы гелия He⁺, лития Li⁺⁺ и т.д.

Рассмотрим систему, состоящую из ядра и электрона. Потенциальная энергия взаимодействия ядра и электрона равна

.

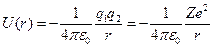Уравнение Шредингера для стационарных состояний электрона в водородоподобном атоме с учетом вида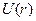

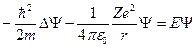, где 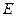- полная энергия электрона;

или

,

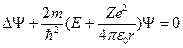где 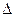- оператор Лапласа:

.

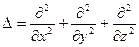Из решения уравнения Шредингера в сферических координатах вытекает существование трех независимых параметров, называемых квантовыми числами. Которые определяют следующие характеристики электрона в атоме.

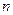- главное квантовое число, оно определяет энергию электрона в атоме.

.

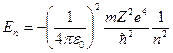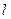- орбитальное (азимутальное) квантовое число, которое определяет момент импульса электрона в атоме, т.е. конфигурацию электронного облака

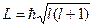
и принимает 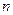значений:

.

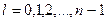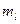- магнитным квантовым числом. Оно определяет проекцию момента импульса на произвольно выбранную ось:

,

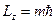и принимает 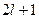значений:

.

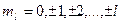Существует еще четвертое квантовое число, существование которого вытекает из решения уравнения Дирака, который в 1929 г. разработал основы релятивистской квантовой механики, откуда вытекает существование собственного механического и магнитного моментов электрона.

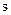- спиновое квантовое число, которое определяет собственный механический момент электрона (спин) и принимает значение ½.

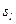- магнитное спиновое квантовое число, которое определяет проекцию собственного механического момента электрона (спина) на произвольно выбранную ось и принимает значение 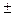½.