Способ Гольдфарба.
Решение основного уравнения метода гармонического баланса (17) относительно амплитуды и частоты автоколебаний можно получить графически.
В способе Гольдфарба, прежде всего, предлагается разрешить основное уравнение относительно частотной характеристики линейной части системы:
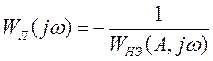 . (18)
. (18)
Затем на комплексной плоскости строятся амплитудно-фазовая характеристика 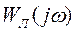 и характеристика, соответствующая нелинейному элементу, т. е. обратная частотная характеристика нелинейного элемента,
и характеристика, соответствующая нелинейному элементу, т. е. обратная частотная характеристика нелинейного элемента,
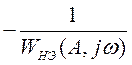 . (19)
. (19)
Если эти две характеристики не пересекаются, то периодических процессов в нелинейной системе не возникает.
При наличии пересечений частота автоколебаний определяется по частотной характеристике линейной части системы 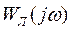 , а амплитуда - по характеристике нелинейного элемента в точке пересечения.
, а амплитуда - по характеристике нелинейного элемента в точке пересечения.
Поскольку в общем случае точек пересечения 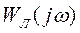 и характеристики нелинейного элемента (19) может быть несколько, в системе могут возникать соответствующие им периодические процессы различных амплитуды и частоты. Причем часть из них будут устойчивыми, а часть - неустойчивыми.
и характеристики нелинейного элемента (19) может быть несколько, в системе могут возникать соответствующие им периодические процессы различных амплитуды и частоты. Причем часть из них будут устойчивыми, а часть - неустойчивыми.
Устойчивость найденного колебательного режима позволяет оценить следующее правило (оно не является строго обоснованным, но зачастую оказывается достаточным). Если при движении по обратной частотной характеристике нелинейного элемента в сторону увеличения амплитуды происходит пересечение амплитудно-фазовой характеристики линейной части «изнутри наружу», то этой точке пересечения соответствуют устойчивые колебания (автоколебания). В противном случае колебания будут неустойчивыми.
На рис. 8 характеристики 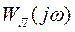 и
и 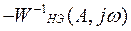 пересекаются в двух точках. Это означает, что в системе могут возникать два вида колебаний.
пересекаются в двух точках. Это означает, что в системе могут возникать два вида колебаний.
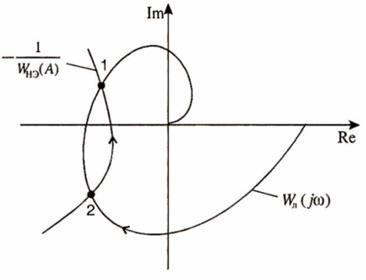
Рис. 8
Причем первой точке пересечения соответствуют устойчивые колебания (автоколебания) с амплитудой A1 и частотой 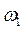 , а второй точке - неустойчивые.
, а второй точке - неустойчивые.
Пример.
Определить параметры колебаний и проверить их устойчивость для системы, изображенной на рис. 6. Здесь нелинейный элемент представляет собой идеальное реле (см. рис. 5) с уровнем ограничения 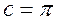 , а передаточная функция линейной части следующая:
, а передаточная функция линейной части следующая:
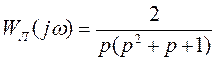 .
.
 Получим выражение для амплитудно-фазовой характеристики (рис. 9) в виде
Получим выражение для амплитудно-фазовой характеристики (рис. 9) в виде
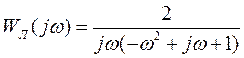 ,
,
или
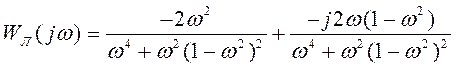 .
.
Запишем выражение для частотной характеристики нелинейного элемента, а затем построим годограф (рис. 9)
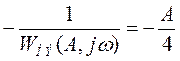 .
.
Как видим, эти характеристики пересекаются в одной точке, которая соответствует автоколебаниям. Для определения их параметров найдем координаты точки пересечения, для чего приравняем нулю мнимую часть 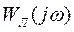 : Рис. 9
: Рис. 9
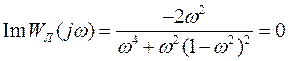 .
.
Отсюда следует, что 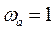 .
.
При найденном значении частоты получим
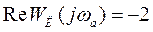 .
.
Из условия
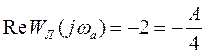 ,
,
определим амплитуду автоколебаний: 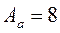 .
.
Дата добавления: 2015-08-14; просмотров: 2996;
