Метод гармонической линеаризации.

Под линеаризацией понимают приближенную замену нелинейной функции линейной таким образом, чтобы по какому-то выбранному показателю обе эти функции совпадали.

В способе гармонической линеаризации нелинейный Рис. 4 элемент заменяется квазилинейным звеном, параметры которого определяются при синусоидальном входном сигнале

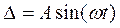(5)

из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена.

Рассмотрим процедуру линеаризации для статического нелинейного элемента, уравнение которого имеет вид

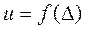. (6)

При поступлении на его вход гармонического сигнала (5) на выходе звена также будет периодический, но несинусоидальный сигнал

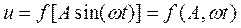. (7)

Разложим его в ряд Фурье и получим

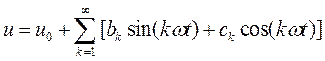, (8)

где будем полагать u₀=0, что справедливо для симметричной нелинейной характеристики (6).

С учетом (7) коэффициенты ряда Фурье (8) определяются известными соотношениями

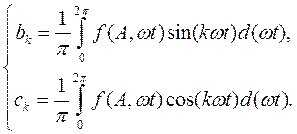
Используем только первые члены ряда разложения в (8), пренебрегая высшими гармониками, и получим

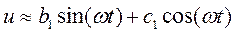. (9)

Учтем, что 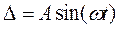, , 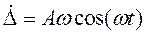следовательно,

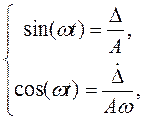(10)

После подстановки (10) в (9) получим выражение для выходного сигнала нелинейного звена, точнее для первой гармоники реакции звена на гармоническое воздействие

,

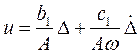которое, если принять обозначения

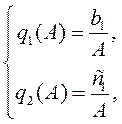(11)

можно записать в виде

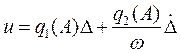. (12)

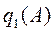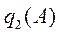Здесь и - коэффициенты гармонической линеаризации, которые зависят только от амплитуды.

Как видим, уравнение нелинейного звена (12) с точностью до высших гармоник является квазилинейным. При постоянных значениях амплитуды входного сигнала А коэффициенты гармонической линеаризации q₁(A) и q₂(A) являются постоянными. Однако различным значениям амплитуды A соответствуют разные коэффициенты q₁(A) и q₂(A). В этом заключается отличие гармонической линеаризации от обычной.

Таким образом, вместо нелинейного элемента с характеристикой (6) можно рассматривать эквивалентное линейное звено, поведение которого описывается уравнением (12). Оно может быть представлено в изображениях по Лапласу

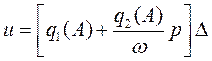. (13)

Для гармонически линеаризованного нелинейного элемента можно записать передаточную функцию

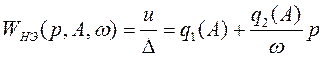, (14)

и получить из нее при 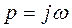выражение для частотной характеристики

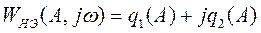. (15)

Для однозначной статической нелинейной характеристики коэффициент

q₂ (A) = 0,

и вместо (15) получим

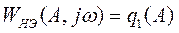, (16)

Коэффициенты гармонической линеаризации типовых статических нелинейных звеньев приводятся в литературе.

Пример. Определить эквивалентную передаточную функцию нелинейного звена, которое представляет собой идеальное реле (рис. 5).

Поскольку идеальное реле имеет однозначную статическую характеристику, выражение для его передаточной функции (16) имеет вид

,

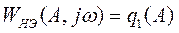где коэффициент q₁(A) определяется как

.

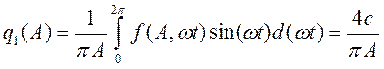Далее, учитывая полученные выражения для передаточной функции гармонически линеаризованного Рис. 5

нелинейного элемента (14), рассмотрим соотношения метода гармонического баланса.