Метод фазовой плоскости.

Метод фазовой плоскости применяется для анализа свойств систем второго порядка и основан на использовании аппарата пространства состояний. Суть метода заключается в отображении частных решений дифференциальных уравнений в совокупность фазовых траекторий.

Обсудим способы построения фазового портрета системы, математическая модель которой имеет вид

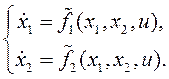(1)

Управляющее воздействие u входит в правую часть (1) как параметр. Отметим, что если оно изменяется, то векторное поле будет управляемым. Здесь полагаем u=const и его численное значение учтем в соответствующих функциях, что позволяет модель (1) записать в форме

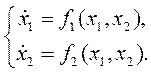(2)

В принципе, задавая множество наборов значений х₁ и x₂, можно получить поле векторов скорости (рис. 1) и, двигаясь вдоль них, построить фазовую траекторию системы из определенных начальных условий.

Таким образом, мы геометрически определили решение дифференциального уравнения (1) для конкретных начальных условий. Однако в настоящее время этот способ не находит применения, так как наличие развитых средств вычислительной техники позволяет получить требуемую совокупность решений.

Например, фазовый портрет можно построить, используя соответствующий пакет прикладных программ SIMULINK.