Основное уравнение метода гармонического баланса.

Если в системе, изображенной на рис. 3,

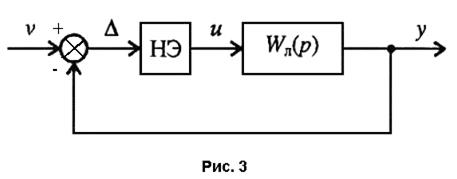
гармонически линеаризовать нелинейный элемент, заменив его эквивалентной передаточной функцией 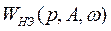, то она становится линейной (гармонически линеаризованной системой) (рис. 6).

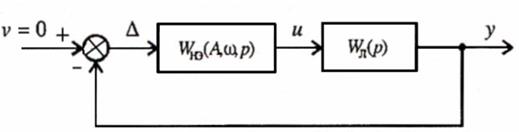
Рис. 6

Следовательно, в этом случае для анализа свойств системы можно применять методы линейной теории управления.

Как известно, в линейной системе (при отсутствии синусоидального сигнала на входе) незатухающие колебания будут возникать лишь в том случае, когда она находится на границе устойчивости. Таким образом, для определения автоколебаний в исходной системе (см. рис. 3) необходимо рассмотреть условие границы устойчивости линеаризованной системы. В соответствии с критерием Найквиста в этой ситуации амплитудно-фазовая характеристика разомкнутой системы должна проходить через точку 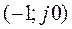, т. е.

.

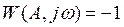Учитывая, что

,

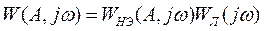запишем условие границы устойчивости в виде

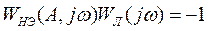. (17)

Это уравнение и представляет собой основное уравнение метода гармонического баланса, из которого можно определить параметры автоколебаний. Если (17) не имеет положительных вещественных решений относительно A и 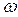, то автоколебательный режим в нелинейной системе не возникает.

Для решения основного уравнения метода гармонического баланса были предложены различные способы, из которых мы рассмотрим лишь способ Гольдфарба