Основные сведения.

Одним из характерных режимов работы нелинейной системы является автоколебательный режим, когда при отсутствии входного сигнала в системе возникают незатухающие периодические процессы, обусловленные начальными условиями. Подобный режим работы может быть требуемым (например, в различных генераторах колебаний) или же к нему сходятся процессы системы.

Прежде всего, нужно исследовать устойчивость нулевого состояния равновесия нелинейной системы, используя метод Ляпунова или метод Попова. Предположим, что ни один из них не гарантирует устойчивость начала координат. Тогда нулевое состояние равновесия может быть неустойчивым. Следующий шаг- рассмотреть возможность возникновения автоколебаний или предельных циклов и определении их параметров (амплитуды и частоты). Для этих целей был разработан регулярный метод, который в русскоязычной литературе получил название метода гармонического баланса. Этот метод применяется для анализа систем с одним нелинейным элементом, причем для простоты будем полагать, что входное воздействие отсутствует (v=0), а все линейные звенья объединены в одно с передаточной функцией W_л(p). Структурная схема рассматриваемых систем изображена на рис. 3.

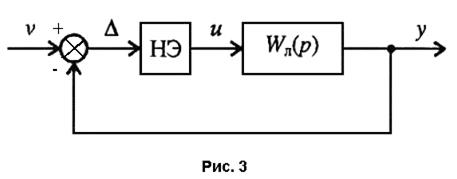
Метод гармонического баланса пригоден для исследования автоколебательных систем практически любого порядка, но требует обеспечения условий хорошей фильтрации возникающих на выходе нелинейного звена гармонических составляющих сигнала (выше первой гармоники).

В основе расчетных соотношений метода гармонического баланса лежит способ гармонической линеаризации нелинейного элемента, который мы далее и рассмотрим.