Невизначений інтеграл та його властивості.

Означення 19.2.Сукупність усіх первісних 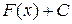на деякому проміжку для функції 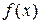називається невизначеним інтегралом і позначається:

,

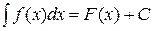(19.7)

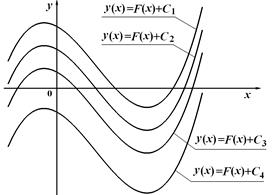Рис. 19.1. До геометричного змісту невизначеного інтеграла

Зауваження 19.1.Геометричний зміст невизначеного інтеграла полягає у тому, що його вираз (19.7) визначає однопараметрич-ну (С – параметр) сім’ю плоских кривих 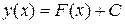. Усі криві такої сім’ї можуть бути отримані одна з одної шляхом паралельного переносу вздовж осі Оу (рис. 19.1).