Алгоритмы сглаживания изображений.
Пусть все весовые коэффициенты равны
1 / (n × m), где n × m – произведение количества строк и столбцов окрестности, т.е. количество элементов множества S. Рассмотрим типичные примеры линейной фильтрации.
В принципе любой фильтр с неотрицательными коэффициентами обладает сглаживающими свойствами. Можно предложить следующие сглаживающие маски [65]:
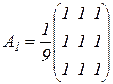 ,
, 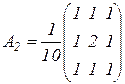 ,
, 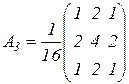 .
.
Коэффициенты масок нормированы с тем, чтобы процедура подавления помех не вызывала смещения яркости исходного изображения. В этом случае выполняется равенство:
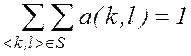 , (1.7)
, (1.7)
где a(k, l) = ak,l – значение весового коэффициента в точке окрестности S с координатами (k, l). Заметим, что если сумма заданных весовых коэффициентов меньше 1, то яркость уменьшится, если больше 1, то яркость увеличится.
Аналитически метод обработки с учетом весовых коэффициентов окрестности можно описать следующим выражением:
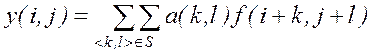 . (1.8)
. (1.8)
Такая модель характерна не только для методов сглаживания, но и для многих других, например для методов увеличения резкости – по назначению противоположных для методов сглаживания. В этом случае обычно весовой коэффициент рабочей точки равен 1, а коэффициенты остальных элементов отрицательны и в сумме составляют -1. Для усиления действия методов помимо повторной обработки применяют больший разброс значений коэффициентов, а также использование окрестности большего размера.
Оператор Собеля. Как классический пример выделения контуров.
Оператор состоит из двух частей: X-оператор и Y-оператор – которые представляют собой две соответствующие матрицы чисел 3 × 3 (рис. 1.3) [3]:
| -1 | ||
| -2 | ||
| -1 |
| -1 | -2 | -1 |
а) б)
Рис. 1.3. Операторы Собеля:
а) Х-оператор Собеля;
б) Y-оператор Собеля
Каждая матрица является экземпляром множества S с рабочей точкой, соответствующей центральному пикселю. Х-оператор Собеля, дает величину горизонтальной составляющей градиента яркости в центральной точке этой матрицы, а Y-оператор – величину вертикальной составляющей градиента. Градиент функции яркости здесь представляет собой результат пространственного дифференцирования, а именно направление наибыстрейшего роста функции в данной точке. В непрерывных системах модуль (длина вектора) градиента выражается следующей формулой:
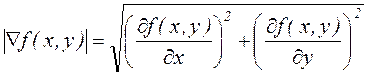 , (1.9)
, (1.9)
где 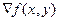 – градиент функции яркости f(x, y) в точке (x, y);
– градиент функции яркости f(x, y) в точке (x, y);
x, y – пространственные координаты плоскости xOy.
В отношении дискретных систем, X- и Y- операторы Собеля являются своеобразной дискретной аппроксимацией входящих в правую часть выражения (1.9) частных производных по дx и дy соответственно.
Обработка каждого пикселя изображения происходит сначала одним оператором, затем другим:
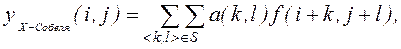 (1.10)
(1.10)
где 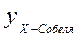 – результат обработки X-оператором Собеля.
– результат обработки X-оператором Собеля.
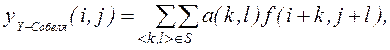 (1.11)
(1.11)
где 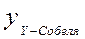 – результат обработки Y-оператором Собеля.
– результат обработки Y-оператором Собеля.
Как видно, выражения (1.10) и (1.11) практически не отличаются от (1.8), за исключением того, что получаемый результат не является конечным. Далее происходит вычисление собственно градиента:
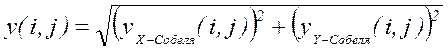 . (1.12)
. (1.12)
Выражение (1.12) аналогично (1.9).
Метод Собеля используют для того, чтобы обнаруживать в изображении резкие переходы, при этом значение каждого пикселя изображения устанавливается в зависимости от градиента (крутизны изменения) яркости в данной точке. В однотонных участках изображения, где все пиксели имеют примерно одинаковую яркость, градиент уровней яркости низок, и в результирующем изображении подобные участки становятся темными. Там же, где имеются резкие переходы (края), крутизна изменения уровней яркости высока, и в конечном изображении в таких участках получаются яркие линии.
Дата добавления: 2015-08-14; просмотров: 1612;
