Преобразование Хаара

(http://habrahabr.ru/post/168517/)

Итак, наша цель — преобразовать изображение так, чтобы оно хорошо сжималось классическими алгоритмами. Подумаем, как нужно изменить его, чтобы получить длинные цепочки нулей.

У «реальных» изображений, таких как фотографии, есть одна особенность — яркость соседних пикселей обычно отличается на небольшую величину. В самом деле, в мире редко можно увидеть резкие, контрастные перепады яркости. А если они и есть, то занимают лишь малую часть изображения.

Рассмотрим фрагмент первой строки яркостей из известного изображения «Lenna» (на рисунке).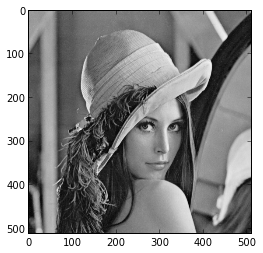

Видно, что соседние числа очень близки. Чтобы получить желаемые нули или хотя бы что-то близкое к ним, можно закодировать отдельно первое число, а потом рассматривать лишь отличия каждого числа от предыдущего.

Получаем:

Уже лучше! Такой метод в самом деле используется и называется дельта-кодированием. Но у него есть серьёзные недостаток — он нелокальный. То есть нельзя взять кусочек последовательности и узнать, какие именно яркости в нём закодированы без декодирования всех значений перед этим кусочком.

Попробуем поступить иначе. Не будем пытаться сразу получить хорошую последовательность, попробуем улучшить её хотя бы немного.

Для этого разобьём все числа на пары и найдём полусуммы и полуразности значений в каждой из них.

Почему именно полусуммы и полуразности? А всё очень просто! Полусумма — это среднее значение яркости пары пикселей. А полуразность несёт в себе информацию об отличиях между значениями в паре. Очевидно, зная полусумму a и полуразность d можно найти и сами значения:
первое значение в паре = a — d,
второе значение в паре = a + d.

Это преобразование было предложено в 1909 году Альфредом Хааром и носит его имя.