Основные свойства многомерных цифровых систем.

1. Устойчивость. Многомерная цифровая система называется устойчивой, если ее свободное движение (15)

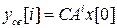
с течением времени затухает, т.е., если

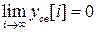(39)

и неустойчивой в противном случае. Во избежание недоразумений надо отметить, что нуль в выражении (39) обозначает нулевой l - вектор, другими словами, система устойчива, если все компоненты l - вектора 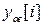с течением времени стремиться к нулю.

Из (15) следует, что условием устойчивости цифровой системы будет стремление к нулю всех элементов матрицы , т.е. условие

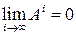. (40)

Здесь нуль обозначает нулевую матрицу ( ).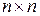

Мы показали, что

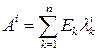, (41)

где 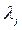, , 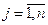собственные значения матрицы А, другими словами, корни характеристического уравнения цифровой системы

.

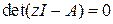Следует заметить, что представление (41) возможно, если все собственные значения 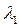, , 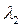…, 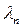являются различными.

С учетом (41) условие устойчивости (40) можно записать в виде

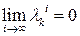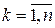, , (42)

при выполнении которого матрица стремится к нулевой матрице. Из (42) следует, что свободное движение цифровой системы с течением времени затухает, если модули всех собственных значений матрицы А меньше единицы, т.е. если

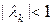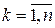, . (43)

Условие (41) является необходимым и достаточным условием устойчивости многомерной цифровой системы.

Вывод. Для устойчивости цифровой системы управления необходимо и достаточно, чтобы все корни 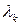, , 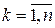ее характеристического уравнения 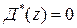имели модули меньше единицы. Если хотя бы один из корней уравнения 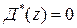имеет модуль больше единицы, то и, следовательно, цифровая система является неустойчивой.

Размещая все корни 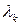на комплексной плоскости корней характеристического уравнения 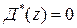(рис.16), легко прийти к геометрической трактовке условий устойчивости:

1. Для устойчивости замкнутой цифровой системы управления необходимо и достаточно, чтобы все корни ее характеристического уравнения располагались внутри окружности единичного радиуса комплексной плоскости Z .

2. Если хотя бы один из корней характеристического уравнения 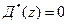расположен за пределами этой окружности, то такая цифровая система является неустойчивой.

3. Если один или несколько корней 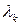располагаются на окружности единичного радиуса, а остальные - внутри этой окружности, то цифровая система находится на границе устойчивости.

4. Если характеристическое уравнение цифровой системы 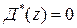содержит единичный корень 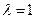кратности 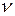, , а остальные корни имеют модули меньше единицы, то такая система называется нейтрально устойчивой. Нейтральная устойчивость означает, что 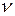-я разность свободного движения 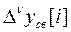с течением времени затухает, т.е. система устойчива по отношению к этой разности.