Форми запису задачі лінійного програмування і її економічна інтерпретація
Приклад задачі ЛП
Для виготовлення трьох видів виробів А, У и С використається чотири види встаткування. Витрати часу на обробку одного виробу для кожного з видів устаткування зазначені в таблиці. У ній же зазначений загальний фонд робочого часу кожного з видів устаткування й прибуток від реалізації кожного з видів виробу.
| Тип устаткування | Витрати часу на обробку одного виробу (станко-год) | Загальний фонд робочого часу устаткування (год) | ||
| А | В | С | ||
| I II III IV | ||||
| Прибуток (грн) |
Потрібно визначити, скільки виробів і якого виду варто виготовити підприємству, щоб прибуток від їхньої реалізації була максимальною.
Складемо математичну модель задачі.
Нехай виготовлено 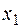 виробів А,
виробів А, 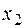 виробів В,
виробів В, 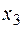 виробів С.
виробів С.
Тоді для виробництва такої кількості виробів потрібно 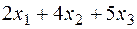 станко-годинника встаткування виду I. З урахуванням загального фонду робочого часу цього встаткування маємо
станко-годинника встаткування виду I. З урахуванням загального фонду робочого часу цього встаткування маємо 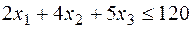 .
.
Міркуючи аналогічно, одержимо систему обмежень
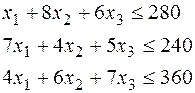
При цьому, тому що кількість вироблених виробів є величина позитивна, те 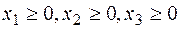 .
.
Прибуток від реалізації 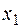 виробів А,
виробів А, 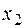 виробів У и
виробів У и 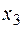 виробів З ми дістанемо прибуток
виробів З ми дістанемо прибуток
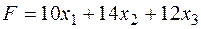
Таким чином, одержуємо задачу ЛП
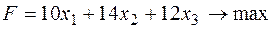
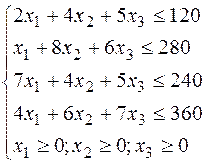
Загальною задачею ЛП називається задача, що складається у визначенні максимального (мінімального) значення функції
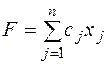 (2.9)
(2.9)
при умовах 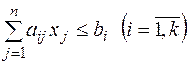 (2.10)
(2.10)
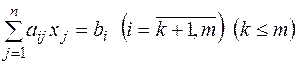 (2.11)
(2.11)
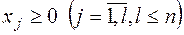 (2.12)
(2.12)
де 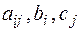 – задані постійні величини.
– задані постійні величини.
Функція (1) називається цільовою функцією (або лінійною формою) задачі (1) -(4), умови (2) -(4) – обмеженнями даної задачі.
Стандартної (або симетричної) задачею лінійного програмування називається задача, що складається у визначенні max функції 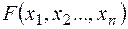 при виконанні умов (2) і (4), де
при виконанні умов (2) і (4), де 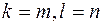 , тобто
, тобто
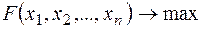
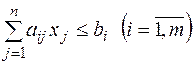
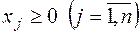
Канонічної (або основний) задачею ЛП називається задача, що складається у визначенні максимального значення функції 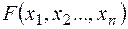 при виконанні умов (3), (4), де
при виконанні умов (3), (4), де  , тобто
, тобто
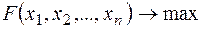
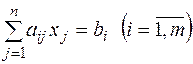
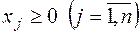
Сукупність чисел 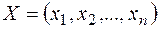 , що задовольняє обмеженням (2) -(4), називається припустимим рішенням (або планом).
, що задовольняє обмеженням (2) -(4), називається припустимим рішенням (або планом).
План 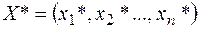 , при якому цільова функція (1) приймає своє max (min) значення, називається оптимальним. Значення цільової функції при плані
, при якому цільова функція (1) приймає своє max (min) значення, називається оптимальним. Значення цільової функції при плані 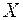 позначаємо
позначаємо 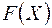 . Отже
. Отже 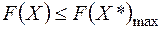
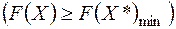 .
.
Основна, стандартна й канонічна є еквівалентними. Т.е. з однієї форми можна шляхом деяких перетворень одержати іншу. І якщо маємо спосіб рішення однієї із задач, то можна знайти оптимальний план інших.
Для того, щоб перейти від однієї форми задачі ЛП до інший, потрібно:
– переходити від задачі min до задачі max
– переходити від обмежень-нерівностей до обмежень-рівностей і навпаки
– заміняти змінні, які не підкоряються умовам незаперечності.
1) У випадку, коли потрібно знайти 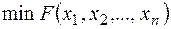 можна перейти до знаходження максимуму функції
можна перейти до знаходження максимуму функції 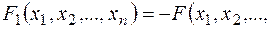
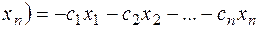 , оскільки
, оскільки 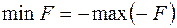
2) Обмеження-нерівності вихідної задачі, що мають вид 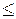 , можна перетворити в обмеження-рівності додаванням до його лівої частини додатковій ненегативної змінної.
, можна перетворити в обмеження-рівності додаванням до його лівої частини додатковій ненегативної змінної.
Для обмежень виду 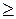 приводять до обмеження-рівності вирахуванням з його лівої частини додаткової ненегативної змінної. Т. е. обмеження-нерівності
приводять до обмеження-рівності вирахуванням з його лівої частини додаткової ненегативної змінної. Т. е. обмеження-нерівності  перетворять в обмеження
перетворять в обмеження 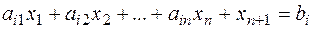 ; обмеження
; обмеження 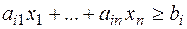 приводяться до обмежень
приводяться до обмежень 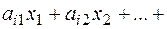
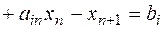 , де
, де 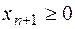 .
.
З іншого боку, обмеження-рівності 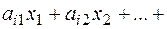
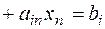 приводяться до системи нерівностей
приводяться до системи нерівностей
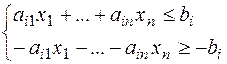
Число вводи додаткових ненегативних змінних при перетворенні обмежень-нерівностей до обмежень-рівностей дорівнює числу самих нерівностей.
Вводи додаткові змінні мають цілком певний економічний зміст. Так, якщо в обмеженнях вихідної задачі ЛП відбивається витрата й наявність виробничих ресурсів, то числове значення додаткової змінної дорівнює об'єму невикористованого відповідного ресурсу.
Приклад. Приведемо розглянуту задачу до канонічного виду: 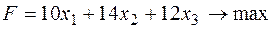
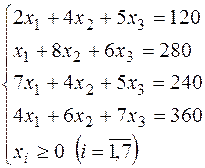
Тут, приміром, 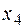 – кількість невикористаного часу встаткування типу I.
– кількість невикористаного часу встаткування типу I.
Дата добавления: 2015-08-14; просмотров: 1280;
