ЛЕКЦІЯ №2
| Тема: | Основи лінійного програмування | ||
| ПЛАН 2.1. Принцип оптимальності в плануванні і керуванні, загальна задача оптимального керування 2.2. Форми запису задачі лінійного програмування та її економічна інтерпретація 2.3. Геометрична інтерпретація задачі | |||
| Час: | 4 год. | ||
| Література: | [1] с. 20-66. | ||
2.1. Принцип оптимальності в плануванні й керуванні, загальна задача оптимального програмування
Лінійне програмування— це приватний розділ оптимального програмування. У свою чергу оптимальне (математичне) програмування— розділ прикладної математики, що вивчає задачі умовної оптимізації. В економіці такі задачі виникають при практичній реалізації принципу оптимальності в плануванні й керуванні.
Необхідною умовою використання оптимального підходу до планування й керування (принципу оптимальності) є гнучкість, альтернативність виробничо-господарських ситуацій, в умовах яких доводиться приймати планово-управлінські рішення. Саме такі ситуації, як правило, і становлять повсякденну практику господарюючого суб'єкта (вибір виробничої програми, прикріплення до постачальників, маршрутизація, розкрій матеріалів, готування сумішей і т.д.).
Суть принципу оптимальності складається в прагненні вибрати таке планово-управлінське рішення 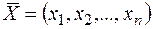 , де
, де 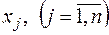 - його компонента, що щонайкраще враховувало б внутрішні можливості й зовнішні умови виробничої діяльності господарюючого суб'єкта.
- його компонента, що щонайкраще враховувало б внутрішні можливості й зовнішні умови виробничої діяльності господарюючого суб'єкта.
Слову «щонайкраще» тут означають вибір деякого критерію оптимальності, тобто деякого економічного показника, що дозволяє порівнювати ефективність тих або інших планово-управлінських рішень. Традиційні критерії оптимальності: «максимум прибутку», «мінімум витрат», «максимум рентабельності» і ін.
Слова «ураховувало б внутрішні можливості й зовнішні умови виробничої діяльності» означають, що на вибір планово-управлінського рішення (поводження) накладається ряд умов, тобто вибір 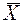 здійснюється з деякої області можливих (припустимих) рішень
здійснюється з деякої області можливих (припустимих) рішень 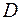 ; цю область називають також областю визначення задачі.
; цю область називають також областю визначення задачі.
Таким чином, реалізувати на практиці принцип оптимальності в плануванні й керуванні - це значить вирішити екстремальну задачу виду:
 , (2.1)
, (2.1)
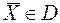 , (2.2)
, (2.2)
де 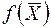 – математичний запис критерію оптимальності – цільова функція. Задачу умовної оптимізації (2.1), (2.2) звичайно записують у вигляді:
– математичний запис критерію оптимальності – цільова функція. Задачу умовної оптимізації (2.1), (2.2) звичайно записують у вигляді:
Знайти максимум або мінімум функції
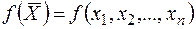 (2.3)
(2.3)
при обмеженнях
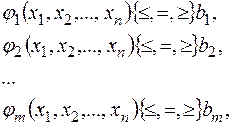 (2.4)
(2.4)
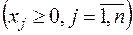 . (2.5)
. (2.5)
Умова (2.5) необов'язково, але його завжди при необхідності можна домогтися. Позначення {<,=,>} говорить про те, що в конкретному обмеженні можливий один зі знаків: <,= або >. Більше компактний запис:
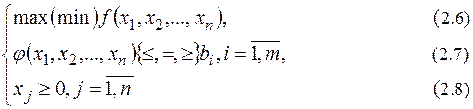
Задача (2.6)-(2.8) - загальна задача оптимального (математичного) програмування, інакше - математична модель задачі оптимального програмування, в основі побудови (розробки) якої лежать принципи оптимальності й системності.
Вектор 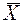 (набір керуючих змінних
(набір керуючих змінних 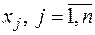 ) називається припустимим рішенням, або планом задачі оптимального програмування, якщо він задовольняє системі обмежень. А той план
) називається припустимим рішенням, або планом задачі оптимального програмування, якщо він задовольняє системі обмежень. А той план 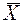 (припустиме рішення), що доставляє максимум або мінімум цільової функції
(припустиме рішення), що доставляє максимум або мінімум цільової функції 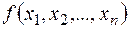 ,називається оптимальним планом (оптимальним поводженням, або просто рішенням) задачі оптимального програмування.
,називається оптимальним планом (оптимальним поводженням, або просто рішенням) задачі оптимального програмування.
Таким чином, вибір оптимального управлінського поводження в конкретній виробничій ситуації пов'язаний із проведенням з позицій системності й оптимальності економіко-математичного моделювання й рішенням задачі оптимального програмування.
Задачі оптимального програмування в найбільш загальному виді класифікують по наступних ознаках.
1) По характері взаємозв'язку між змінними:
а) лінійні;
б) нелінійні.
У випадку а) всі функціональні зв'язки в системі обмежень і функція мети - лінійні функції; наявність нелінійності хоча б в одному зі згаданих елементів приводить до випадку б).
2) По характері зміни змінних:
а) безперервні;
б) дискретні.
У випадку а) значення кожної з керуючих змінних можуть заповнювати суцільно деяку область дійсних чисел; у випадку б) всі або хоча б один змінна можуть приймати тільки цілочислові значення.
3) По обліку фактору часу:
а) статичні;
б) динамічні.
У задачах а) моделювання й прийняття рішень здійснюються в припущенні про незалежність від часу елементів моделі протягом періоду часу, на який приймається планово-управлінське рішення. У випадку б) таке припущення досить аргументовано прийняте не може бути й необхідно враховувати фактор часу.
4) По наявності інформації про змінні:
а) задачі в умовах повної визначеності (детерміновані);
б) задачі в умовах неповної інформації;
в) задачі в умовах невизначеності.
У задачах б) окремі елементи є імовірнісними величинами, однак відомі або додаткові статистичні дослідження можуть бути встановлені їхні закони розподілу. У випадку в) можна зробити припущення про можливий ісходах випадкових елементів, але немає можливості зробити висновок про ймовірності ісходів.
5) По числу критеріїв оцінки альтернатив:
а) прості, однокритеріальні задачі;
б) складні, багатокритеріальні задачі.
У задачах а) економічно прийнятне використання одного критерію оптимальності або вдається спеціальними процедурами (наприклад, «зважуванням пріоритетів») звести багатокритеріальний пошук до однокритериального; приклади багатокритеріальних задач розглянуті в гл. 3.
Сполучення ознак 1-5 дозволяє групувати (класифікувати) у самому загальному виді задачі й методи оптимального програмування, наприклад: 1а),2а),3а),4а),5а) - задачі й методи лінійного програмування; 1б),2а),3а),4а),5а) - задачі й методи нелінійного програмування;1а),2б),3а),4а),5а) - задачі й методи цилочислового (дискретного) лінійного програмування й т.д.
Дата добавления: 2015-08-14; просмотров: 759;
