Геометрична інтерпретація задачі
Розглянемо основну задачу ЛП: 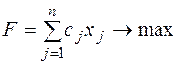 при умовах
при умовах 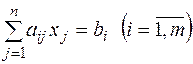 ,
, 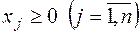 .
.
Розглянемо вектора  , складені з коефіцієнтів при змінних
, складені з коефіцієнтів при змінних 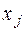 у системі обмежень
у системі обмежень
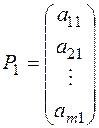 ,
, 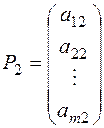 , …,
, …, 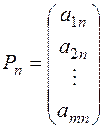 и.
и. 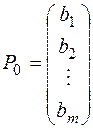
План 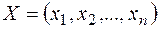 називається опорним планом основної ЗЛП, якщо система векторів
називається опорним планом основної ЗЛП, якщо система векторів 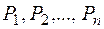 лінійно незалежна.
лінійно незалежна.
Нагадаємо, що система векторів лінійно незалежна, якщо визначник, складений з координат цієї системи векторів відмінний від 0, тобто
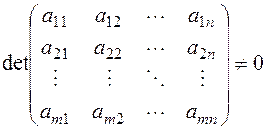 .
.
Тому що розмірність векторів 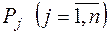 дорівнює
дорівнює 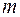 , та максимальна кількість лінійно незалежних векторів дорівнює
, та максимальна кількість лінійно незалежних векторів дорівнює 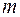 .
.
Опорний план називається невирожденим, якщо він містить рівно 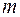 позитивних компонентів
позитивних компонентів 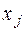 . У противному випадку він є вирожденим.
. У противному випадку він є вирожденим.
Уведемо ряд допоміжних визначень, які мають наочну геометричну характеристику, коли число невідомих дорівнює 2: 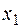 і
і 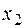 .
.
Множина називається опуклим, якщо разом з будь-якими двома своїми крапками 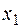 й
й 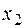 воно містить і їхню лінійну комбінацію
воно містить і їхню лінійну комбінацію 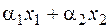 , де
, де 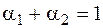 ,
, 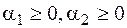 .
.
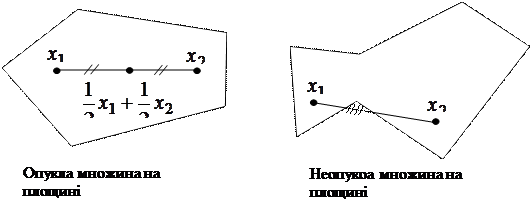
Сформулюємо теорему: Множина планів ЗЛП є опуклим (якщо воно не густо).
Непуста множина планів основний ЗЛП називається багатогранником рішень, а кутова крапка багатогранника рішень називається його вершиною.
Теорема: Якщо ОЗЛП має оптимальний план, то max значення цільова функція задачі приймає в одній з вершин багатогранника рішень. Якщо max значення цільова функція задачі приймає більш, ніж в одній вершині, то вона приймає max у всякій крапці, є лінійною комбінацією цих вершин вид 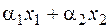 , де
, де 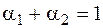 ,
,  ,
, 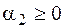 ,
, 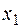 і
і 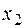 – вершини.
– вершини.
Виходячи із цієї теореми, робимо висновок, що непуста множина планів ОЗЛП утворять опуклий багатогранник. Кожна вершина цього багатогранника утворять опорний план. В одній з вершин багатогранника значення цільової функції є максимальним (за умови, що функція обмежена зверху на множині планів).
Якщо max цільова функція приймає більш, ніж в одній вершині, то це значення вона приймає й на границі багатогранника, що з'єднує ці вершини.
1. Знайдемо рішення задачі у випадку, коли 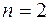 :
:
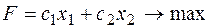 (1)
(1)
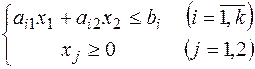 (2)
(2)
Кожному з нерівностей (2) відповідає напівплощина, границею якої є пряма 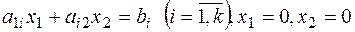 .
.
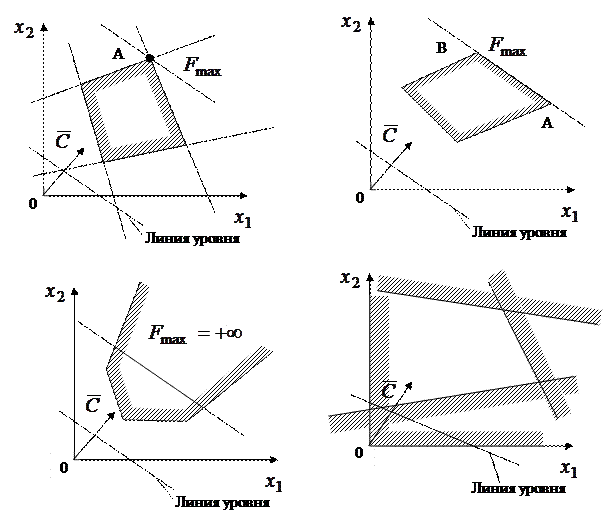
Якщо система нерівностей сумісна, то вона утворить опуклий багатогранник, що у плоскому випадку називається багатокутником рішень.
Сторони багатокутника лежать на зазначених прямих. Таким чином, необхідно знайти вершину багатокутника, у якій цільова функція 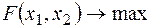 .
.
Для визначення даної вершини побудуємо пряму 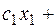
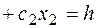 (
( 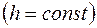 – лінія рівня), що проходить через багатокутник рішень. Будемо пересувати її в напрямку вектора
– лінія рівня), що проходить через багатокутник рішень. Будемо пересувати її в напрямку вектора 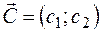 доти, поки вона не пройде через останню її загальну крапку з багатокутником рішень. Координати цієї крапки й визначають оптимальний план задачі.
доти, поки вона не пройде через останню її загальну крапку з багатокутником рішень. Координати цієї крапки й визначають оптимальний план задачі.
 |
Відзначимо, що для знаходження 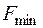 лінію рівня
лінію рівня 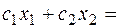
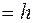 необхідно пересувати убік вектора
необхідно пересувати убік вектора 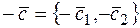 .
.
Общий алгоритм:
1. Будують прямі, рівняння яких одержують із нерівностей системи обмежень заміною знаків нерівностей на знаки рівностей.
2. Знаходять напівплощини, обумовлені кожним з обмежень.
3. Знаходять багатокутник рішень.
4. Будують вектор 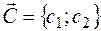 .
.
5. Будують пряму 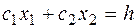 , що проходить через багатокутник рішень.
, що проходить через багатокутник рішень.
6. Пересувають пряму 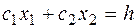 в напрямку вектора
в напрямку вектора 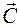 . У результаті знаходять крапку (крапки), у якій цільова функція приймає max значення.
. У результаті знаходять крапку (крапки), у якій цільова функція приймає max значення.
7. Визначаємо координати т. max і обчислюємо значення цільової функції в цій т. 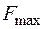 .
.
Приклад.
А й В - види виробу, на виробництво яких потрібне сировина трьох видів I, II, III. У таблиці наведені норми витрати сировини кожного виду на виготовлення одиниці продукції даного виду й прибуток від реалізації кожного з виробів А, В. Потрібно скласти такий план їхнього випуску, що прибуток підприємства від їхньої реалізації була максимальна.
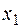 – кількість випущеного виробу А.
– кількість випущеного виробу А.
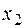 – кількість випущеного виробу В.
– кількість випущеного виробу В.
| Види сировини | Норми витрати на один виріб | Загальна кількість сировини | |
| А | В | ||
| I II III | |||
| Прибуток від реалізації |
Постановка задачі.
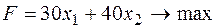
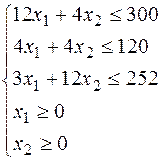
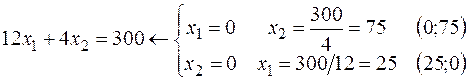
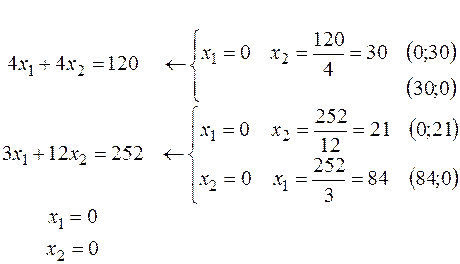
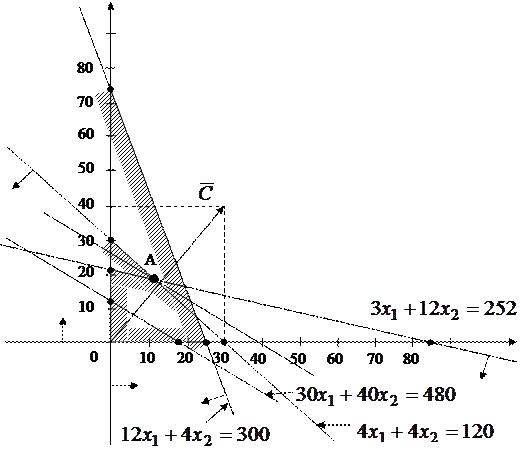
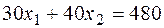 – (лінія рівня) – будь-яка крапка цій прямій визначає такий план, при якому прибуток дорівнює 480 грн.
– (лінія рівня) – будь-яка крапка цій прямій визначає такий план, при якому прибуток дорівнює 480 грн.
4) 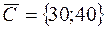
5) 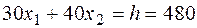
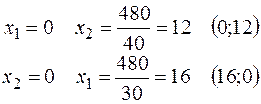
6) Рухаючи пряму рівня паралельно прямій 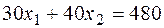 уздовж вектора
уздовж вектора 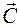 одержуємо крапку А, координати цієї крапки
одержуємо крапку А, координати цієї крапки 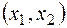 й визначають оптимальний план. А знаходимо вирішуючи систему рівнянь, які визначають прямі - сторони багатокутника.
й визначають оптимальний план. А знаходимо вирішуючи систему рівнянь, які визначають прямі - сторони багатокутника.
7) 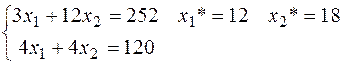
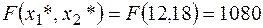 – max прибуток, 12 виробів А, 18 виробів В.
– max прибуток, 12 виробів А, 18 виробів В.
Дата добавления: 2015-08-14; просмотров: 1040;
