Загальна характеристика задач динамічного програмування і їх геометрична й економічна інтерпретації.

У розглянутих вище задачах лінійного й нелінійного програмування ми знаходили рішення як би в один етап або за один крок. Такі задачі одержали назву одноетапних або однокрокових.

На відміну від цих задач задачі динамічного програмування є багатоетапними або багатокроковими. Іншими словами, знаходження рішення конкретних задач методами динамічного програмування включає кілька етапів або кроків, на кожному з яких визначається рішення деякої приватної задачі, обумовленої вихідної. Тому термін «динамічне програмування» не стільки визначає особливий тип задач, скільки характеризує методи знаходження рішення окремих класів задач математичного програмування, які можуть ставитися до задач як лінійного, так і нелінійного програмування. Незважаючи на це, доцільно дати загальну постановку задачі динамічного програмування й визначити єдиний підхід до її рішення.

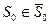Запропонуємо, що дана фізична система перебуває в деякому початковому стані і є керованою. Таким чином, завдяки здійсненню деякого керування 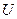зазначена система переходить із початкового стану 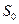в кінцевий стан 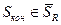. При цьому якість кожного з реалізованих керувань 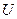характеризується відповідним значенням функції . Завдання полягає в тому, щоб із множини можливих керувань 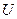знайти таке 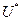, при якому функція приймає екстремальне (максимальне або мінімальне) значення . Сформульована задача і є загальною задачею динамічного програмування.

Дамо геометричну інтерпретацію цієї задачі. Припустимо, що стан системи характеризується деякою точкою на площині 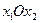й цій точці завдяки здійснюваному керуванню її рухом переміщається уздовж лінії, зображеної на мал. 1, з області можливих початкових станів 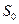в область припустимих кінцевих станів 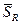Кожному керуванню 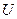рухом точки, поставимо у відповідність значення деякої функції (наприклад, довжину шляху, пройденого точкою під впливом даного керування). Тоді завдання полягає в тім, щоб із всіх припустимих траєкторій руху точки знайти таку, котра виходить у результаті реалізації керування 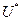, що забезпечує екстремальне значення функції . До визначення такої «траєкторії» зводиться й задача динамічного програмування у випадку, коли припустимі стани системи визначаються точками 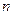-мірного простору.

Економічну інтерпретацію загальної задачі динамічного програмування розглянемо на конкретних прикладах.

Для збільшення об'ємів випуску продукції, що користується підвищеним попитом, виготовленої підприємствами, виділені капіталовкладення в об'ємі тис. руб. із зазначених засобів забезпечує приріст випуску продукції, обумовлений значенням нелінійної 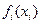функції .

Знайти розподіл капіталовкладень між підприємствами, що забезпечує максимальне збільшення випуску продукції.

Розв’язання. Математична постановка задачі складається у визначенні найбільшого значення функції

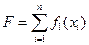(1)

при умовах

(2)

(3)

Сформульована задача є задачею нелінійного програмування. У тому випадку, коли 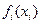- опуклі (або ввігнуті) функції, її рішення можна знайти, наприклад, методом множників Лагранжа. Якщо ж функції 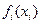не є такими, то відомі методи знаходження рішення задач нелінійного програмування не дозволяють визначити глобальний максимум функції (1). Тоді рішення задачі (1) – (3) можна знайти за допомогою динамічного програмування. Для цього вихідну задачу потрібно розглянути як багатоетапну або багатокрокову. Замість того щоб розглядати припустимі варіанти розподілу капіталовкладень між 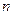підприємствами й оцінювати їхня ефективність, будемо досліджувати ефективність вкладення засобів на одному підприємстві (1-крок), на двох підприємствах (2-й крок) і т.д., нарешті, на 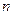підприємствах. Таким чином, одержимо 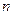етапів, на кожному з яких стан системи (у якості якої виступають підприємства) описується об'ємом засобів, що підлягають освоєнню підприємствами . 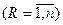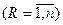Рішення про об'єми капіталовкладень, виділюваних -му підприємству , і є керуваннями. Завдання полягає у виборі таких керувань, при яких функція (1) приймає найбільше значення.