Решение. Поиск критических путей

Поиск критических путей

1) Построим график привязки (рис.17).

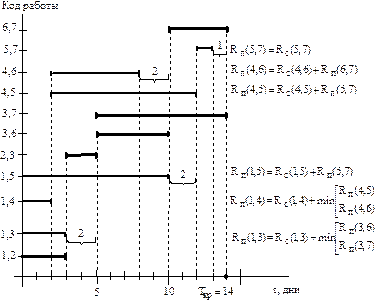
Рис.17 - График привязки задачи 3

2) Начнем поиск критических путей (справа налево) с работ, завершающих проект. На графике привязки две работы (6,7) и (3,7), которые заканчиваются позже остальных в завершающем событии 7. Записываем работы, определенные как критические справа налево:

;

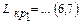(1)

.

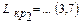3) Найдем критическую работу из 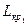, предшествующую (6,7). Код этой работы должен оканчиваться на 6. Таких работ две – (4,6) и (3,6). Но только одна из них, работа (3,6) по времени своего окончания вплотную "примыкает" на графике к началу работы (6,7). Допишем слева найденную критическую работу (3,6) к выражению (1)

.

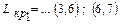(2)

4) Найдем критическую работу из 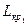, предшествующую (3,6). Код этой работы должен оканчиваться на 3. Таких работ две – (2,3) и (1,3). Но только одна из них, работа (2,3) по времени своего окончания вплотную "примыкает" на графике к началу работы (3,6). Допишем слева найденную критическую работу (2,3) к выражению (2)

.

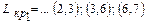(3)

5) Найдем критическую работу из 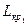, предшествующую (2,3). Код этой работы должен оканчиваться на 2. Работа (1,2) по времени своего окончания вплотную "примыкает" на графике к началу работы (2,3). С этой работы начинается критический путь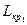

.

6) Аналогичный поиск работ критического пути 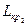приводит к результату .

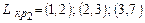В другой форме записи 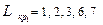и .

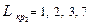7) Для наглядности выделим на графике привязки критические работы жирной линией.

Поиск резервов работ

1) Для всех найденных критических работ впишем в таблицу 25 нулевые значения свободного и полного резервов. Рассмотрим некритические работы, начиная с конца таблицы.

Таблица 25 - Резервы работ из задачи 2

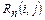
				Критичность
1,2				Критическая
1,3				–
1,4				–
1,5				–
2,3				Критическая
3,6				Критическая
3,7				Критическая
4,5				–
4,6				–
5,7				–
6,7				Критическая

2) Работа (5,7), согласно графику привязки (см. рис. 17), заканчивается в 13-й день, а завершающее событие 7 сети, в которое она входит, наступает лишь в 14-й день. Т.е. если работа (5,7) задержится на 1 день, то это не повлияет на срок выполнения проекта ( 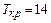дней). Поскольку (5,7) завершающая работа сети, то ее полный и свободный резервы равны .

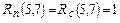3) Работа (4,6) заканчивается в 8-й день, в то время как последующая работа (6,7) начинается в 10-й день. То есть, работа (4,6) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (6,7), т.е. .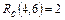

За работой (4,6) следует только критическая работа (6,7) с нулевым полным резервом:

.

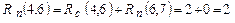4) Работа (4,5) заканчивается в 12-й день, в этот же день начинается следующая работа (5,7), т.е. любая задержка выполнения работы (4,5) приведет к задержке начала работы (5,7). Это означает, что работа (4,5) не имеет свободного резерва 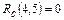. Но если сдвинуть во времени работу (4,5) на 1 день, то работа (5,7) также сдвинется на 1 день и это не нарушит срок выполнения проекта, т.к. у работы (5,7) есть временной резерв:

5) Работа (1,5) заканчивается в 10-й день, в то время как последующая работа (5,7) начинается в 12-й день. Работа (1,5) может задержаться на 2 дня и это не повлияет на время начала последующей работы (5,7), т.е. 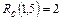. Кроме того, поскольку последующая работа (5,7) имеет резерв в 1 день, то, в общем, работу (1,5) можно сдвинуть на 3 дня и это не нарушит сроков проекта (см. рис.9.4):

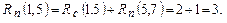
6) Работа (1,4) заканчивается во 2-й день, и в этот же день начинаются следующие работы (4,5) и (4,6). Работа (1,4) не имеет свободного резерва времени 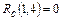. Поскольку после работы (1,4) следуют две работы с различными полными резервами, то:

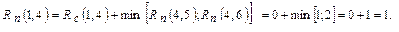7) Работа (1,3) заканчивается в 3-й день, а следующие за ней работы (3,6) и (3,7) начинаются в 5-й день, т.е. 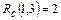. Поскольку обе последующие работы критические, то полный и свободный резерв работы (1,3) совпадают:

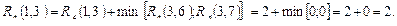8) Ненулевые свободные резервы работ обозначены на графике привязки фигурными скобками (см. рис. 17).