И моделей в системах массового обслуживания

Системы массового обслуживания (СМО) - это системы, в которых возникают массовые запросы (требования) на выполнение каких-либо услуг и происходит удовлетворение этих запросов. СМО включает в себя следующие элементы: источник требований, входящий поток требований, очередь, обслуживающие устройства (каналы обслуживания), выходящий поток требований. Исследованием таких систем занимается теория массового обслуживания.

Методами теории массового обслуживания могут быть решены многие задачи исследования процессов, происходящих в экономике. В организации сельского хозяйства эти методы позволяют определить оптимальное количество животноводческих подразделений, численность работников, частоту завоза кормов и другие параметры. Другим характерным примером систем массового обслуживания могут служить склады снабженческо-сбытовых подразделений. Задача теории массового обслуживания в данном случае сводится к тому, чтобы установить оптимальное соотношение между числом поступающих на склад требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными.

Классификация СМО.

1. В зависимости от условий ожидания начала обслуживания различают:

• СМО с потерями (отказами);

• СМО с ожиданием.

В СМО с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и теряются. Классическим примером системы с отказами является телефонная станция. Если вызываемый абонент занят, то требование на соединение с ним получает отказ и теряется.

В СМО с ожиданием требование, застав все обслуживающие каналы занятыми, становится в очередь и ожидает, пока не освободится один из обслуживающих каналов.

СМО, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ограниченной длиной очереди.

СМО, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.

2. По числу каналов обслуживания СМО делятся на:

· одноканальные;

· многоканальные.

3. По месту нахождения источника требований СМО делятся на:

· разомкнутые, когда источник требования находится вне системы;

· замкнутые, когда источник находится в самой системе.

Примером разомкнутой системы может служить предприятие по ремонту сельскохозяйственной техники. Здесь неисправные тракторы– это источник требований на их обслуживание, находятся вне самой системы, число требований можно считать неограниченным. К замкнутым СМО относится, например, станочный участок, в котором станки являются источником неисправностей, а, следовательно, источником требований на их обслуживание, например, бригадой наладчиков.

Методы и модели, применяющиеся в теории массового обслуживания, можно условно разделить на аналитические и имитационные.

Аналитические методы теории массового обслуживания позволяют получить характеристики системы как некоторые функции параметров ее функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффективность работы СМО.

Имитационные методы основаны на моделировании процессов массового обслуживания на ЭВМ и применяются, если невозможно применение аналитических моделей. Далее будем рассматривать аналитические методы моделирования СМО.

В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых входящий поток требований является простейшим (пуассоновским).

Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, т.е. вероятность поступления за время t ровно k требований задается формулой:

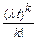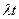P_k(t)= e- . (1)

Простейший поток обладает тремя основными свойствами: ординарности, стационарности и отсутствием последействия.

Ординарность потока означает практическую невозможность одновременного поступления двух и более требований.

Стационарным называется поток, для которого число требований, поступающих в систему в единицу времени, не меняется во времени. Вероятность поступления в систему определенного количества требований в течение заданного промежутка времени зависит от его величины и не зависит от начала его отсчета на оси времени.

Отсутствие последействия означает, что число требований, поступивших в систему до момента t, не определяет того, сколько требований поступит в систему за промежуток времени от t до t + D t.

Важная характеристика СМО – время обслуживания требований в системе. Время обслуживания одного требования является случайной величиной. Наибольшее распространение получил экспоненциальный закон распределения времени обслуживания. Функция распределения для этого закона имеет вид:

F(t)=1 – e , (2)

т.е. вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой (2), где 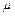– параметр экспоненциального закона распределения времени обслуживания требований в системе, т.е. величина, обратная среднему времени обслуживания – t_об:

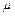=1/t_об (3)

Рассмотрим аналитические модели наиболее распространенных СМО с ожиданием, т.е. таких СМО, в которых требования, поступившие в момент, когда все обслуживающие каналы заняты, ставятся в очередь и обслуживаются по мере освобождения каналов.

Общая постановка задачи состоит в следующем. Система имеет n обслуживающих каналов, каждый из которых может одновременно обслуживать только одно требование.

В систему поступает простейший (пуассоновский) поток требований. Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания.

Время обслуживания каждого требования t_об – случайная величина, которая подчиняется экспоненциальному закону распределения с параметром .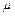

СМО с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. К замкнутым относятся системы, в которых поступающий поток требований возникает в самой системе и ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится потенциальным источником требований на накладку. В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно.