График взаимосвязи работ во времени

Для проведения анализа временных параметров сетевой модели используют график привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси – отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ).

Временные параметры работ определяются на основе ранних и поздних сроков событий:

· – ранний срок начала работы;

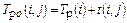· – ранний срок окончания работы;

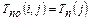· – поздний срок окончания работы;

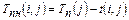· – поздний срок начала работы.

График привязки можно построить на основе данных о продолжительности работ. При этом необходимо учитывать, что работа 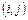может выполняться только после того, как будут выполнены все предшествующие ей работы .

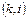При поиске критических путей выявляют критические работы. Признаком критической работы являются нулевые значения резервов времени. Это означает, что каждая последующая критическая работа будет начинаться строго в момент окончания предыдущей критической работы. Вследствие этого сдвиг любой из работ критического пути обязательно приведет к увеличению первоначальной длительности проекта ( 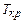). Критический путь является полным, т.е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.

Способ определения критического пути на графике привязки (все найденные работы выписываются последовательно справа налево):

1) найти на графике привязки и выписать работу (i,j), которая заканчивается позже всех остальных. Это будет последняя работа критического пути (ее конечное событие иметь номер завершающего события сети);

2) из всех работ сети (k,i), конечное событие которых i совпадает с начальным событием i работы (i,j), найденной в п.1), выбрать и выписать ту, которая на графике вплотную примыкает к работе (i,j);

3) из всех работ сети (l,k), конечное событие которых k совпадает с начальным событием k работы (k,i), найденной в п.2), выбрать и выписать ту, которая на графике вплотную примыкает к работе (k,i);

4) продолжать п.3) до тех пор, пока не будет найдена исходная работа сети, т.е. начинающаяся в нулевой момент времени (ее начальное событие будет иметь номер исходного события сети, например, 1).

Если в сетевой модели несколько критических путей, то, используя приведенный алгоритм, можно обнаружить несколько работ, удовлетворяющих сформулированным требованиям. В таком случае необходимо продолжать поиск по каждой из таких работ в отдельности. В сложных сетевых моделях подобные разветвления могут привести к большим затратам времени на поиск критических путей. Графический способ используется для относительно простых сетевых моделей. Преимущество этого способа в его наглядности.

Для поиска резервов работ используется следующее правило: полный резерв любой работы складывается из собственного свободного резерва и минимального из полных резервов непосредственно следующих работ.