Модели разомкнутых систем
Если число требований на обслуживание бесконечно, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины. Для этих систем поступающий поток требований можно считать неограниченным.
Отмеченные особенности функционирования систем этих двух видов накладывают определенные условия на используемый математический аппарат. Расчет характеристик работы СМО различного вида может быть проведен на основе расчета вероятностей состояний СМО (так называемые формулы Эрланга).
Рассмотрим алгоритмы расчета показателей качества функционирования разомкнутой системы массового обслуживания с ожиданием.
При изучении таких систем рассчитывают различные показатели эффективности обслуживающей системы. В качестве основных показателей могут быть вероятность того, что все каналы свободны или заняты, математическое ожидание длины очереди (средняя длина очереди), коэффициенты занятости и простоя каналов обслуживания и др.
Введем в рассмотрение параметр 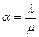 . Если
. Если 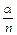 < 1, то очередь не может расти безгранично. Условие
< 1, то очередь не может расти безгранично. Условие 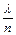 < 1 означает, что число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования.
< 1 означает, что число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования.
Важнейшие характеристики работы СМО:
1. Вероятность того, что все обслуживающие каналы свободны:
 (4)
(4)
2. Вероятность того, что занято ровно k обслуживающих каналов при условии, что общее число требований, находящихся на обслуживании, не превосходит числа обслуживающих каналов:
Pk= 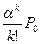 при 1
при 1 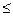 k
k 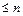 (5)
(5)
3. Вероятность того, что в системе находится k требований в случае, когда их число больше числа обслуживающих каналов:
Pk= 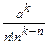 Po при k
Po при k 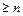 (6)
(6)
4. Вероятность того, что все обслуживающие каналы заняты:
Pk=  Po; (a / n<1) (7)
Po; (a / n<1) (7)
5. Средняя длина очереди:
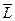 оч=
оч= 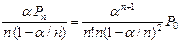 ; (a / n<1) (8)
; (a / n<1) (8)
6. Среднее число свободных от обслуживания каналов:
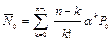 (9)
(9)
7. Коэффициент простоя каналов:
Kпр=  (10)
(10)
8. Среднее число занятых обслуживанием каналов:
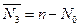 (11)
(11)
9. Коэффициент загрузки каналов:
К3= 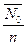 (12)
(12)
Пример. МТС имеет n = 5 бригад по ремонту тракторов. В среднем в течение рабочего дня от сельскохозяйственных предприятий поступает в ремонт 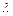 =10 тракторов. Поток заявок на ремонт тракторов является случайным, пуассоновским. Каждый трактор в зависимости от характера неисправности также требует различного случайного времени на ремонт. Время ремонта подчиняется экспоненциальному закону; при этом в среднем в течение рабочего дня каждая из бригад успевает отремонтировать
=10 тракторов. Поток заявок на ремонт тракторов является случайным, пуассоновским. Каждый трактор в зависимости от характера неисправности также требует различного случайного времени на ремонт. Время ремонта подчиняется экспоненциальному закону; при этом в среднем в течение рабочего дня каждая из бригад успевает отремонтировать 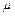 = 2,5 трактора. Требуется оценить работу МТС, рассчитав ряд основных характеристик данной СМО.
= 2,5 трактора. Требуется оценить работу МТС, рассчитав ряд основных характеристик данной СМО.
За единицу времени принимаем 1 рабочий день (7 часов).
1. Определим параметр
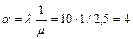
так как 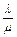 <n, то очередь не может расти безгранично.
<n, то очередь не может расти безгранично.
2. Вероятность того, что все мастера свободны от ремонта тракторов согласно (4).
P0= 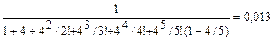
3. Вероятность того, что все бригады заняты ремонтом согласно (7):
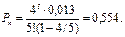
Это означает, что 55,4% времени бригады полностью загружены работой.
4. Среднее время обслуживания (ремонта) одного трактора согласно (3):
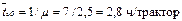
(при условии семичасового рабочего дня).
5. Очень важной характеристикой является средняя длина очереди, которая определяет необходимое место для хранения тракторов, требующих ремонта; находим ее по (8):
трактора 
6. Определим среднее число бригад, свободных от работы, по (9):
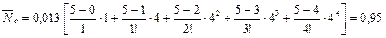
Таким образом, в среднем в течение рабочего дня ремонтом заняты четыре бригады из пяти.
Дата добавления: 2015-08-14; просмотров: 745;
