Предельная ошибка выборки.
В конкретной выборке действительная ошибка может быть больше средней, меньше средней или равна средней. Каждое из этих расхождений имеет определенную вероятность.
 | |||
 | |||
Предельная ошибка выборки – это максимальное различие между выборочной и генеральной характеристикой, гарантируемое с определенной вероятностью.
где t – нормированное отклонение, зависящее от вероятности, определяемое как аргумент интегральной функции Лапласа Ф(t). Определение предельной ошибки выборки основано на теореме Чебышева –Ляпунова.
Теорема Чебышева-Ляпунова:
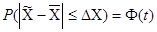 |
С вероятностью сколь угодно близкой к единице можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии выборочная характеристика будет очень мало отличаться от генеральной характеристики.
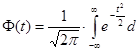 |
Значение этой функций находиться в таблице, поэтому, зная вероятность P =Ф(t), можно определить аргумент t.
Наиболее часто используемые значения приведем в таблице:
| Р(t) | 0,683 | 0,95 | 0,954 | 0,99 | 0,997 |
| t | 1,96 | 2,58 |
Чем больше вероятность, с которой гарантируются результаты, тем больше будет предельная ошибка и менее надежные результаты выборки. Поэтому в экономических исследованиях используется Р=0,95 и Р=0,954.
Дата добавления: 2015-08-14; просмотров: 765;
