Соотношение между амплитудами и фазами падающей, отражённой и преломлённой волн.
Рассмотрим случай нормального падения световой волны на границу раздела двух сред с n1 и n2. Е, E' и E’’ – напряжённости электрического поля в падающей, отражённой и преломлённой волнах.
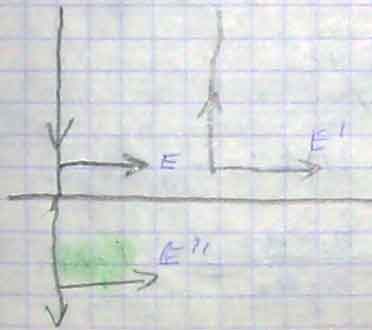
Из курса электричества известно, что тангенсальная составляющая вектора напряжённости электрического поля не прерывается при переходе через границу, поэтому для данного случая можно записать:
E+E’=E’’ (1)
Используем ЗСЭ.
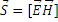 – вектор Поинтига представляет собой плотность потока энергии. S=EH=
– вектор Поинтига представляет собой плотность потока энергии. S=EH= 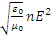 . (2)
. (2)
Из ЗСЕ: S=S’+S’’ (3).
Подставляя (2) в (3):  Отсюда учитывая (1):
Отсюда учитывая (1): 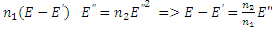 .
.
Т.к. 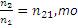
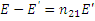 . (5)
. (5)
Получена система уравнений (1) и (5), из которой найдём E’ и E’’.
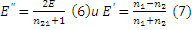 .
.
Из (6) видно, что т.к.  , то E’’ и E имеют одинаковые знаки. Это значит, что фаза волны не изменяется при преломлении. Из (7) видно, что если волна падает из оптически более плотной в оптически менее плотную, т.е. n1>n2, то
, то E’’ и E имеют одинаковые знаки. Это значит, что фаза волны не изменяется при преломлении. Из (7) видно, что если волна падает из оптически более плотной в оптически менее плотную, т.е. n1>n2, то 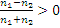 и при отражении от такой границы фаза отражённой волны постоянна (E’ и E – одинаковые знаки). Если волна падает на более оптически плотную среду, т.е. n1<n2, то
и при отражении от такой границы фаза отражённой волны постоянна (E’ и E – одинаковые знаки). Если волна падает на более оптически плотную среду, т.е. n1<n2, то 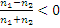 => E и E’ – противоположных знаков => при отражении волны из оптически более плотной среды, её фаза скачком меняется на Пи.
=> E и E’ – противоположных знаков => при отражении волны из оптически более плотной среды, её фаза скачком меняется на Пи.
Найдём выражение для коэффициента отражения R и коэффициента пропускания Т. R представляет собой долю отражённой энергии и равен отношению интенсивности отражённой волны к интенсивности падающей волны: R=I’/I (8).
Т представляет собой отношение преломлённой волны к интенсивности падающей: T=I’’/I (9).
Интенсивность прямо пропорциональна квадрату амплитуды электрического поля: I - 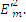 (10)
(10)
Используя (10) и (8) имеем:
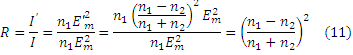
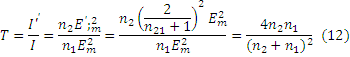
Дата добавления: 2015-08-14; просмотров: 2722;
