Отражение и преломление плоской волны на границе двух диэлектриков. Законы отражения и преломления света.
Рассмотрим падение плоской световой волны на границе раздела двух прозрачных (не поглощающих) сред с показателями преломления n1 и n2. В этом случае происходит преломление и отражение света. Вывод закона преломления и отражения удобно проводить с помощью принципа Гюйгенса: каждая точка волнового фронта становится источником вторичных сферических волн и новым фронтом волны является огибающая этих вторичных волн.
Рассмотрим преломление света.
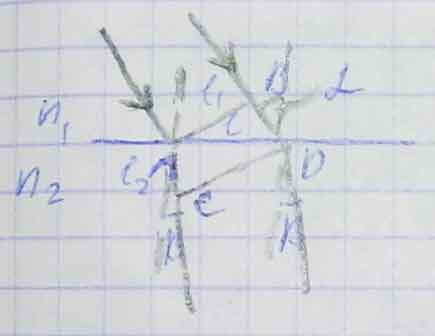
α – угол падения. BD=L1, AC=L2, AD=L. В первой среде световая волна движется с V1, а во второй с V2. Расстояние L1 и L2 волна проходит за время t =>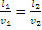 
(1) . Из ABD и ACD: 
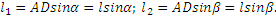(2). Отсюда 
. => 
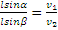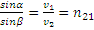(3).
Формула (3) представляет собой запись закона преломления света: луч падающий, луч преломлённый и нормаль границ раздела сред в точке падения лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления – величина постоянная для данных сред и называется относительным показателем преломления или показателем преломления второй среды относительно первой.
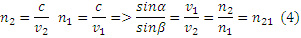
Совершенно аналогично используя принцип Гюйгенса можно показать, что угол падения равен углу отражения, что является основой закона отражения: луч падающий, луч отражённый и нормаль границы раздела сред в точке падения лежат в одной плоскости. Угол падения равен углу отражения. Причём падающие отражённые лучи лежат по разные стороны нормали.
Среду, у которой показатель преломления больше, называют оптически более плотной. Из закона преломления (4) видно, что при падении луча из оптически менее плотной в оптически более плотную среду (n2>n1) α>β.
Если увеличить α, то мы получим прямой угол β.
Луч падает из оптически более плотной в менее плотную среду (n2<n1) α<β.
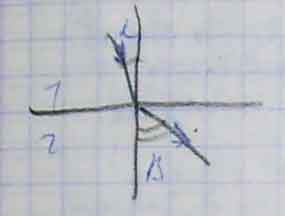
При некотором αкр преломлённый луч становится скользящим (β=90°).
Если α>αкр, то наблюдается явление полного внутреннего отражения. Предельный αкр находится:
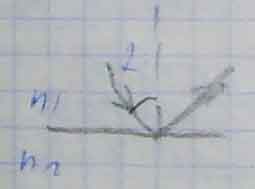
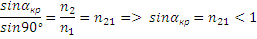
При переходе из одной среды в другую наряду со скоростью волны меняется и λ в n21 раз, а частота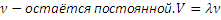 
.
Дата добавления: 2015-08-14; просмотров: 1940;